Доведення. Нехай найвищий порядок мінорів, що не дорівнюють нулю є число р

Нехай найвищий порядок мінорів, що не дорівнюють нулю є число р. Це означає, що в матриці А є мінор р-того порядку, не рівний нулю. Мінори р + 1 і більш високих порядків дорівнюють нулю.

Для визначеності припустимо, що мінор р-того порядку не рівний нулю знаходиться в лівому верхньому куту.

М

Треба довести, що ранг матриці дорівнює р.

Для цього треба довести два факти:

1) в матриці А є р-лінійно-незалежних стовпців;

2) всі інші стовпці через них лінійно виражаються.

1) Доведемо, що лінійно незалежними (за нашим припущенням) є перші р стовпців матриці. Припустимо супротивне, що перші р стовпців матриці лінійно залежні. Тоді з означення лінійної залежності випливає, що існують числа , що виконується рівність:

Розглянемо цю рівність покомпонентно:

І компонента -

р компонента -

………………………………………………

компонента -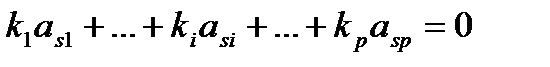

З перших р рівностей випливає що стовпці мінора М - лінійно залежні. Доведемо, що тоді мінор М дорівнює нулю.

Розглянемо два випадки.

а) р = 1 тобто М = - лінійно залежний, а звідси випливає що .

б) р≥2 В цьому випадку лінійна залежність означає, що в мінорі М існує стовпець, що є лінійною комбінацією інших стовпців, а тоді за властивістю визначників мінор М = 0

Отже, ми прийшли до суперечності умові. Отже, перші р стовпців матриці А- лінійно незалежні.

Для доведення другого факту побудуємо визначник.

i=1,2,…,s k=p+1,…n

Доведемо, що при всіх таких і та к визначник

Для доведення розглянемо два випадки:

1) 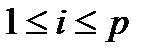. В цьому випадку як визначник з двома рівними рядками.

2) 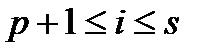. В цьому випадку , бо визначник стає мінором р + 1 порядку матриці А, а тоді за умовою, він дорівнює нулю.

Розкладемо визначник за останнім рядком:

.

Розв'яжемо цю рівність відносно ,

.

Надамо всі значення

Це означає, що к- тий стовпець матриці А є лінійною комбінацією перших р-стовпців. Оскільки к набуває значень , то ми довели, що всі стовпці, починаючи з р + 1 є лінійними комбінаціями перших р- стовпців.

Що і треба було довести

Таким чином за означенням ранг дорівнює р.

Наслідки з теореми про ранг: