Доведення. Для зручності доведення цієї властивості введемо символ

Для зручності доведення цієї властивості введемо символ .

Нехай задано суму однотипних доданків

Застосовуючи двічі цей символ, отримаєм для

Доведемо таку властивість:

Для цього доведемо, що . Для доведення проведемо підсумування за стовпцями

Отже

Тепер перейдемо до доведення попередньої властивості транзитивності.

Нехай задано системи:

(1)

(3)

(2)

За умовою (1) лінійно виражається через (2). Тоді за означенням - є лінійною комбінацією векторів системи (2)

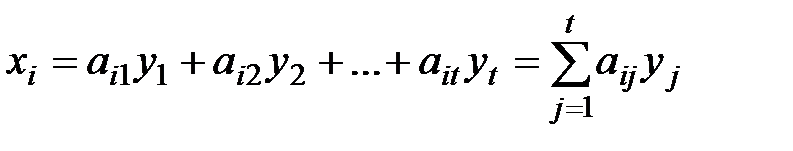(i=1,2,…,S) (4)

За умовою (2) лінійно виражається через (3), тому

Підставимо (5) в (4), тоді отримаємо

Отже доведено, що система векторів (1) лінійно виражається через систему (3).

Наслідок. Якщо система векторів (1) еквівалентна системі (2), а система (2) еквівалентна системі (3), то системи (1) і (3) еквівалентні.

Транзитивність еквівалентних систем доводиться повторенням двічі наведених міркувань.