Доведення. Нехай задано довільний визначник:

Нехай задано довільний визначник:

Доведемо, що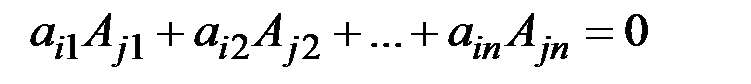

Для доведення побудуємо допоміжний визначник, який буде відрізнятися від визначника d лише одним рядком.

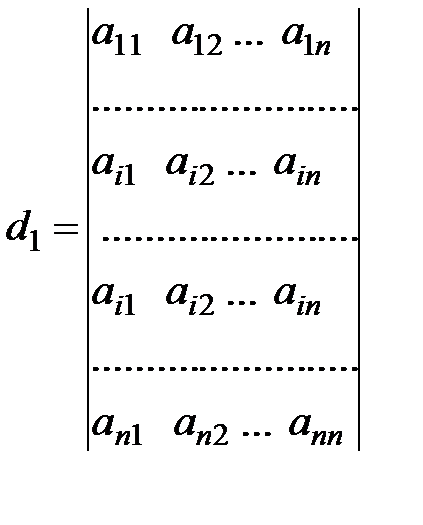
Цей визначник за властивістю 4 дорівнює 0.

Застосуємо до j-го рядка визначника наслідок з теореми Лапласа.

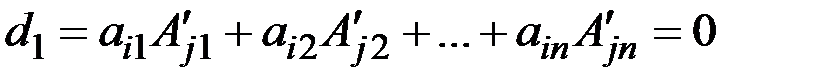
Залишилось довести, що 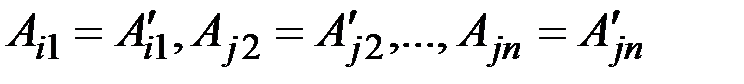. Ці рівності випливають з того, що при побудові алгебраїчних доповнень до елементів j-го рядка цей рядок викреслюється, а визначники d і d₁ відрізняються лише j-тим рядком.

Означення. Визначником системи називається визначник складений з коефіцієнтів при невідомих.

Теорема Крамера. Нехай задано систему n алгебраїчних рівнянь з n невідомими, визначник якої не нульовий. Тоді невідома x_k дорівнює дробу, знаменником якого є визначник системи, а чисельником також є визначник, який можна отримати з визначника системи заміною k-го стовпця стовпцем вільних членів.

Доведення. Розглянемо систему

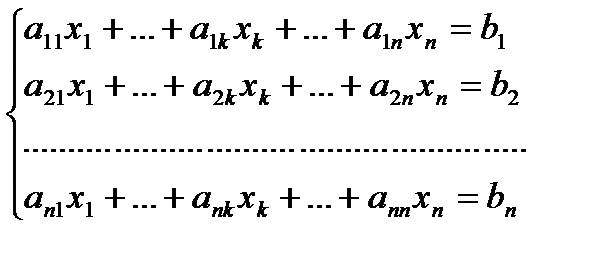(1)
з визначником системи

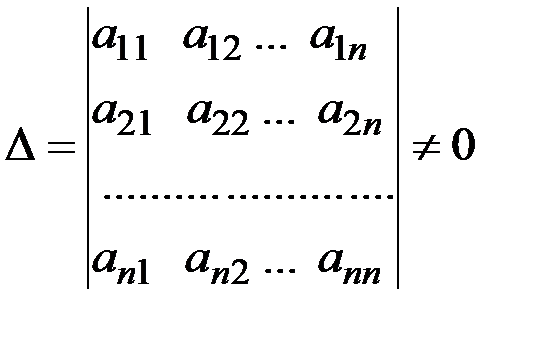(2)

Помножимо обидві частини 1-го рівняння на А_1k, 2-го на А_2k, n-го на А_nk.

Тоді отримаємо

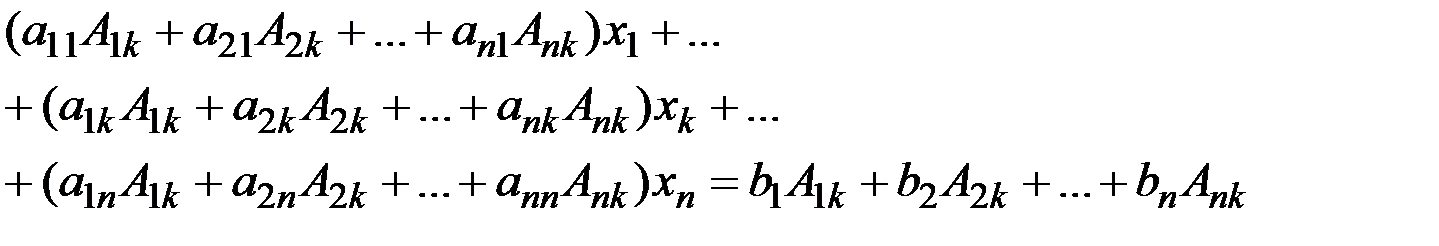
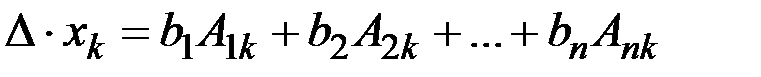k=1,2,…,n (3)

Введемо в розгляд деякий визначник.

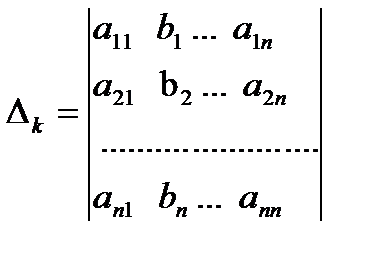
Застосуємо до k-го рядка цього визначника наслідок теореми Лапласа

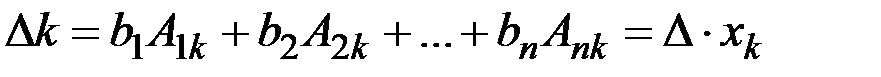
Застосуємо лему, тоді з рівності (3) маємо

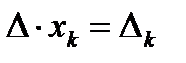
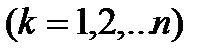
Отже

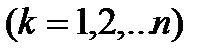
Теорему Крамера доведено.