Дифференцирование интеграла, зависящего от параметра

Из курса действительного анализа известно, что интеграл, зависящий от параметра, можно дифференцировать под знаком интеграла, если производная подынтегральной функции по параметру непрерывна.

Пусть обладает следующими свойствами:

1. Û

2. , по совокупности аргументов Û .

При этих условиях существует

Докажем, что 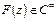, причем производную 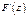можно искать дифференцируя под знаком интеграла.

Из курса действительного анализа известно, что действительный интеграл, зависящий от параметра, можно дифференцировать под знаком интеграла, если производная подынтегральной функции по параметру непрерывна. Поэтому

Кроме того, Þ 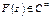, причем

,

т.е. производную можно искать, дифференцируя под знаком интеграла.