Признаки сходимости рядов с неотрицательными членами

Основные понятия.

Определение. Если ряд из модулей сходится, то ряд исходный ряд называется абсолютно сходящимся.

Теорема 10.1. Если ряд сходится абсолютно, то он сходится в обычном смысле.

Доказательство.

Если ряд из модулей сходится, то для него выполнен критерий Коши Þ "e>0 $ N (e): <e для " n>N и " m 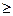0, но | a_n+a_n+1+…+a_n+m| <e Þ для исходного ряда также выполнен критерий Коши и он сходится.

Обратное, вообще говоря, неверно.

Определение. Если сам ряд сходится, а соответствующий ряд из модулей расходится, то ряд называется условно сходящимся.

Из свойств неубывающих последовательностей Þ

Лемма. Для того, чтобы ряд с неотрицательными членами сходился необходимо и достаточно, чтобы последовательность его частичных сумм была бы ограниченна сверху, причем, если S =sup{ }, то S – сумма ряда.

Пример.

=

Т.о. у ряда с положительными членами ограничена последовательность частичных сумм Þ ряд сходится.

2. Признаки сравнения для рядов с неотрицательными членами.

Теорема 10.2. (Первый признак сравнения) Пусть a_n ³ 0, b_n ³ 0 и a_n = O (b_n). Тогда

1) если ряд сходится, то сходится и ряд ;

2) если же расходится ряд , то расходится и ряд .

Доказательство.

По определению a_n = O (b_n) ó $0< c <¥: a_n £ c b_n, в частности возможно a_n £ b_n.

1. если “больший” ряд сходится Þ ограничена последовательность его частичных сумм £ M <¥, но тогда последовательность частичных сумм “меньшего” ряда £ cM также ограничена сверху. Тогда по Лемме ряд сходится.

2. Предположим обратное, а именно “больший” ряд 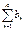сходится, тогда по доказанному в п.1) “меньший” ряд 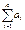должен сходится, а это противоречит условию.

Теорема 10.3. (Второй признак сравнения) Пусть a_n >0, b_n >0 и $ ,0< k <¥. Тогда ряды и сходятся или расходятся одновременно.

Доказательство.

Если $ 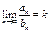,то "e>0 $ N (e): " n > N (e)

ó ó Выбирая e, можем добиться k- e>0. Применяя первый признак сравнения и оценку , получим, что из сходимости ряда следует сходимость ряда . Аналогично используя оценку , из расходимости ряда следует рассходимость ряда .

Примеры.

1. , , а ряд 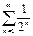сходится – это сумма бесконечно убывающей геометрической прогрессии.

2. , начиная с определенного номера n > N выполнено , а гармонический ряд расходится Þ расходится и исходный ряд.

3. - ряд с неотрицательными членами.

при n ®¥.

Но ряд сходится, значит по первому признаку сравнения сходится и исходный ряд.

4. - ряд с отрицательными членами, но если мы докажем сходимость ряда , то мы тем самым докажем сходимость исходного ряда. при n ®¥ Þ исходный ряд сходится.

5. - ряд с положительными членами, т.к. при n =3,4,… и Þ (под логарифмом стоит число, большее единицы). Учитывая, что при n ®¥, получим асимптотику членов исходного ряда

,

т.о. исходный ряд эквивалентен гармоническому и Þ расходится.