Неопределенный интеграл функции комплексной переменной

Редактор Л. В.Доценко. Ответственный редактор И. В. Пучкова

Технический редактор Е. Ф. Коржуева

Компьютерная верстка: Е. Ю. Матвеева

Корректоры Н.В.Козлова, В.Н.Рейбекель

Изд. № 101110508. Подписано в печать 07.06.2006. Формат 60x90/16. Гарнитура «Тайме». Бумага тип. № 2. Печать офсетная. Усл. печ.л. 14,0. Тираж 3000 экз. Заказ №16865.

Издательский центр «Академия», www.academia-moscow.ru

Санитарно-эпидемиологическое заключение № 77.99.02.953.Д.004796.07.04 от 20.07.2004. 117342, Москва, ул. Бутлерова, 17-Б, к. 360. Тел./факс: (495)330-1092, 334-8337.

Отпечатано в ОАО «Саратовский полиграфический комбинат». 410004, г. Саратов, ул. Чернышевского, 59.

Неопределенный интеграл функции комплексной переменной.

Если g- односвязная и f(z) ÎC^¥(g), то для " z ₁, z ₂Îg не зависит от пути интегрирования Т.о. при фиксированном z ₀ интеграл 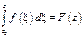- функция только z!

Определение. Пусть g-односвязная область, f (z)ÎC(g) (не обязательно аналитическая!) и для " замкнутого контура gÌg 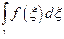=0. Функция 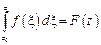- называется неопределенным интегралом от f(z).

Теорема 6.1.

Пусть g-односвязная, f (z)ÎC(g) и для " замкнутого контура gÌg 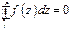, тогда $ 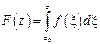, F(z) ÎC^¥(g) и .

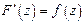Доказательство.

В силу 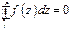для " замкнутого контура 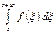не зависит от пути интегрирования => можем взять отрезок прямой, соединяющий точки z и D z

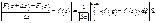
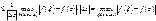
В силу непрерывности f (z) правая часть неравенства может быть сделана меньше "e<0 для =>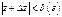

$ .

Т.о. F (z) – неопределенный интеграл от функции комплексного переменного f (z).

И F(z) – аналитическая, т.к. ее производная по условию теоремы непрерывна. § 7. Интегральная формула Коши. Интеграл Коши.