 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Правила вычисления определенного интеграла. 1. Формула Ньютона-Лейбница
|
|
1. Формула Ньютона-Лейбница. Если 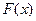 – некоторая первообразная функции
– некоторая первообразная функции 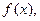 то
то
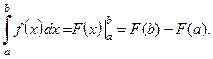
2. Формула замены переменной. Если 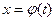 – монотонная непрерывно дифференцируемая для
– монотонная непрерывно дифференцируемая для 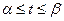 функция, такая, что
функция, такая, что 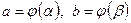 , то
, то
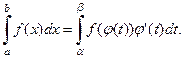
Замечание. При замене переменной в определенном интеграле меняются и пределы интегрирования.
3. Формула интегрирования по частям
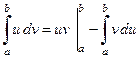 .
.
Пример 4.22. Вычислить интеграл 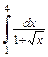 .
.
Решение. Сделаем замену переменной:
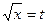 ,
, 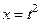 ,
, 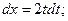
Для пределов интегрирования имеем:
если 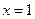 , то
, то 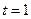 ; если
; если 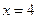 , то
, то 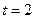 .
.
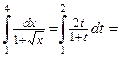
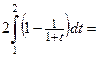
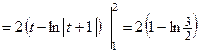 .
.
Пример 4.23. Вычислить интеграл 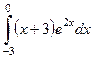 .
.
Решение. Применим формулу интегрирования по частям. Пусть 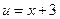 ,
, 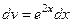 , тогда
, тогда 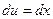 ,
, 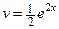 .
.
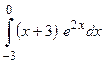
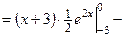
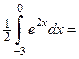
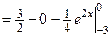
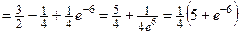 .
.
Дата публикования: 2014-11-19; Прочитано: 236 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
