Несобственные интегралы от неограниченных функций

Если функция 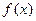имеет бесконечный разрыв в точке , то есть и 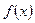непрерывна при , то по определению

, .

Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; в противном случае – расходящимся.

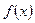Если и непрерывна при 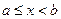, то

, .

Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; в противном случае – расходящимся.

Если , 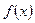и непрерывна при и , то

, .

Пример 4.24. Вычислить интеграл или доказать его расходимость:

Решение.

.

Несобственный интеграл сходится.

Пример 4.25. Вычислить интеграл или доказать его расходимость:

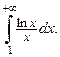
Решение.

.

Несобственный интеграл расходится.

Пример 4.26. Вычислить интеграл или доказать его расходимость:

Решение. Подынтегральная функция 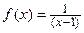в точке 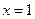имеет бесконечный разрыв, поэтому

.

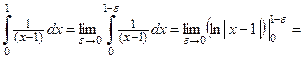
Несобственный интеграл расходится.

Пример 4.27. Вычислить интеграл или доказать его расходимость:

Решение.

.

Данный интеграл сходится.