Интегрирование простейших дробей

1. Интегралы вида .

При

.

При .

2. Интегралы вида .

Рассмотрим случай , то есть .

Сначала выделим в числителе производную знаменателя.

.

.

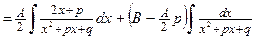Возьмем первый интеграл

.

Второй интеграл сводится к табличному, если в знаменателе выделить полный квадрат.

.

Пример 4.15. Найти интеграл

Решение. Подынтегральная функция является простейшей рациональной дробью первого типа.

Пример 4.16. Найти интеграл

Решение. Подынтегральная функция является простейшей рациональной дробью второго типа. При решении выделим в числителе производную знаменателя.

При интегрировании рациональных дробей с помощью разложения на простейшие дроби следует придерживаться следующей последовательности действий:

1. Если подынтегральная функция является неправильной рациональной дробью, то нужно выделить ее целую часть, то есть представить в виде:

где многочлен, а правильная рациональная дробь.

2. Разложить знаменатель дроби на линейные и квадратичные множители, то есть

где квадратные трехчлены не имеют вещественных корней.

3. Правильную рациональную дробь разложить на Сумму простейших дробей:

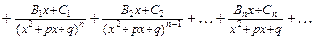
4. Вычислить неопределенные коэффициенты

Пример 4.17. Найти интеграл .

Решение. Имеем Степень многочлена 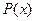равна 1. Степень многочлена 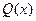равна 3. Значит, подынтегральная дробь правильная. Разложение дроби 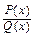на сумму простейших дробей имеет вид:

Найдем неопределенные коэффициенты Для этого правую часть равенства приведем к общему знаменателю.

.

Приравняем числители равных дробей с равными знаменателями.

.

Положим последовательно х равным 1; 2; 3 (корни знаменателя ).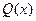

Эти же коэффициенты можно найти другим способом: приравнять коэффициенты при одинаковых степенях х в уравнении

или в уравнении

.

Получим систему уравнений:

Найдем коэффициенты , решив эту систему тем или иным способом: .

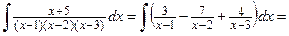
Пример 4.18. Найти интеграл .

Решение. Разложим правильную рациональную дробь на сумму простейших дробей:

= .

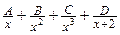Приведем к общему знаменателю правую часть равенства.

= .

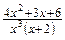Приравнивая числители, получим:

.

Положим : отсюда .

Положим 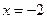: отсюда .

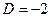Приравняем коэффициенты при и при .

	.

Используя уже найденное значение 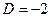, найдем .

=

.

Пример 4.19. Найти интеграл .

Решение. Имеем . Степень многочлена 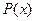равна 3. Степень многочлена 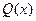равна 3. Значит, подынтегральная функция является неправильной рациональной дробью. Выделим из нее целую часть.

,

разделив столбиком

на ,

получим:

.

Разложим дробь на сумму простейших дробей:

.

Приведем к общему знаменателю правую часть равенства.

.

Приравнивая числители, получим:

.

Положим : отсюда .

Приравняем коэффициенты при и при .

Найдем .

.