Определенный интеграл. Пусть функция определена на отрезке , – некоторое разбиение отрезка

Пусть функция 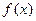определена на отрезке , – некоторое разбиение отрезка на части , и , ,..., – некоторый набор точек. Положим . . Определенным интегралом называется предел интегральных сумм

если он существует и конечен и не зависит от выбора разбиения отрезка на части и выбора точек .

Рис. 23.

Известно, что если функция 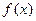непрерывна на отрезке , то

существует.

Геометрический смысл определенного интеграла для случая : площадь криволинейной трапеции ABCD (рис. 23).