 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление площади плоской фигуры. Площадь криволинейной трапеции, ограниченной кривой , где , прямыми и
|
|
Площадь криволинейной трапеции, ограниченной кривой  , где
, где  , прямыми
, прямыми  и
и  и отрезком
и отрезком  оси x (рис. 24), вычисляется по формуле
оси x (рис. 24), вычисляется по формуле


Рис. 24.
Площадь фигуры, ограниченной графиками функций  и
и  (где
(где  ) и прямыми
) и прямыми  и
и  (рис. 25), находится по формуле
(рис. 25), находится по формуле
 .
.

Рис. 25.
Если кривая l задана параметрическими уравнениями 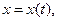
 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми  и
и  и отрезком
и отрезком  оси x, выражается формулой
оси x, выражается формулой

где 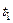 и
и  определяются из условий
определяются из условий  ,
,  . Формула верна, если при
. Формула верна, если при  выполнено неравенство
выполнено неравенство  . Эту же формулу можно применять для вычисления площади фигуры, ограниченной заданной параметрически кривой, то есть в случае, когда
. Эту же формулу можно применять для вычисления площади фигуры, ограниченной заданной параметрически кривой, то есть в случае, когда  и
и  . При этом порядок пределов интегрирования надо выбирать так, чтобы при изменении t от t 1 до t 2 фигура оставалась справа.
. При этом порядок пределов интегрирования надо выбирать так, чтобы при изменении t от t 1 до t 2 фигура оставалась справа.
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением  и двумя лучами
и двумя лучами  (рис. 26), вычисляется по формуле
(рис. 26), вычисляется по формуле
 .
.

Рис. 26.
Замечание. Полярными координатами точки М являются  и
и 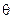 :
:  – полярный радиус (расстояние от точки О, называемой полюсом, до точки М) и
– полярный радиус (расстояние от точки О, называемой полюсом, до точки М) и 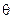 – полярный угол (угол между полярным радиусом и осью Ох) (рис. 27).
– полярный угол (угол между полярным радиусом и осью Ох) (рис. 27).

Рис. 27.
Связь между полярными координатами и декартовыми:
 .
.
Пример 4.28. Вычислить площадь фигуры, ограниченной параболой  и осью
и осью  (рис. 28).
(рис. 28).

Рис. 28.
Решение. Парабола пересекает ось  в точках
в точках 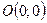 и M (3; 0). Следовательно,
и M (3; 0). Следовательно,
 .
.
Пример 4.29. Вычислить площадь фигуры, ограниченной параболой  и прямой
и прямой  (рис. 29).
(рис. 29).
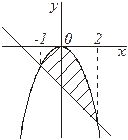
Рис. 29.
Решение. Найдем точки пересечения параболы и прямой, для чего решим систему уравнений: 
 или
или  .
.
Левую часть последнего уравнения можно разложить на множители:  откуда
откуда  , и
, и 
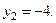 Значит, заданные линии пересекаются в точках
Значит, заданные линии пересекаются в точках  и
и  . Следовательно,
. Следовательно,

 .
.
Пример 4.30. Вычислитьплощадь плоской фигуры, ограниченной кривой

Решение. Кривая является замкнутой, и один оборот проходится при изменении t от  до
до 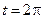 . При этом ограниченная кривой фигура находится справа при таком изменении t. Поэтому, так как
. При этом ограниченная кривой фигура находится справа при таком изменении t. Поэтому, так как
 , и t изменяется от
, и t изменяется от  до
до  . Следовательно,
. Следовательно,







Пример 4.31. Вычислить площадь плоской фигуры, ограниченной кривыми  .
.
Решение. Эти кривые суть окружности радиуса 1 и 2 соответственно, касающиеся в точке (0; 0) (рис. 30).

Рис. 30.
Так как по определению  то
то  и, значит, угол
и, значит, угол 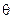 меняется от
меняется от  до
до  . Тогда
. Тогда

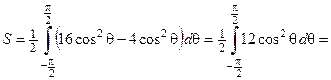

Дата публикования: 2014-11-19; Прочитано: 472 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
