 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Интегрирование по частям. Формула интегрирования по частям:
|
|
Формула интегрирования по частям:
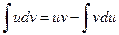 .
.
Обычно выражение 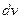 выбирается так, чтобы его интегрирование не вызывало особых затруднений. За
выбирается так, чтобы его интегрирование не вызывало особых затруднений. За 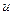 , как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида
, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида
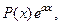
| 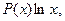
|
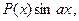
| 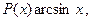
|
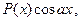
| 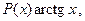
|
где 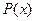 – многочлен от x.
– многочлен от x.
Пример 4.11. 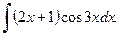
Решение. Положим 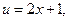
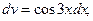 отсюда найдем
отсюда найдем 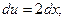
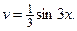
Применим формулу интегрирования по частям:
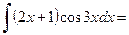
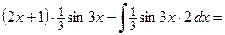
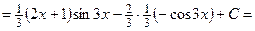
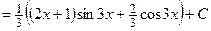 .
.
Пример 4.12. Найти интеграл 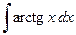 .
.
Решение. Пусть 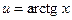 ,
, 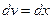 , тогда
, тогда 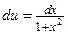 ,
, 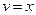 . По формуле интегрирования по частям имеем:
. По формуле интегрирования по частям имеем:
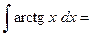
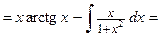
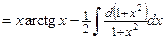
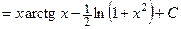 .
.
Пример 4.13. Найти интеграл 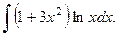
Решение. Пусть 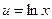 ,
, 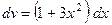 , тогда
, тогда 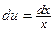 ,
, 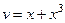 . Воспользуемся формулой интегрирования по частям:
. Воспользуемся формулой интегрирования по частям:
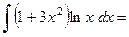
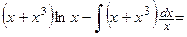
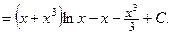
Пример 4.14. Найти интеграл 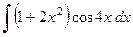 .
.
Решение. Обозначим 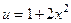 ,
, 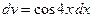 , тогда
, тогда 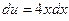 ,
, 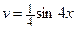 . По формуле интегрирования по частям имеем:
. По формуле интегрирования по частям имеем:
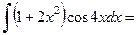
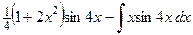 .
.
К последнему интегралу вновь применим формулу интегрирования по частям: 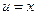 ,
, 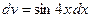 ;
; 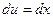 ,
, 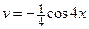 .
.
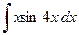
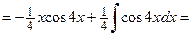
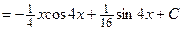 .
.
Окончательно получим
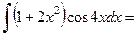
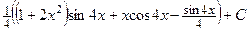 .
.
Дата публикования: 2014-11-19; Прочитано: 230 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
