Взаимное расположение двух плоскостей. Пересекающиеся плоскости A1x + B1y + C1z + D1 = 0 (6.5.1)

Пересекающиеся плоскости A₁x + B₁y + C₁z + D₁ = 0 (6.5.1)

и A₂x + B₂y + C₂z + D₂ = 0 (6.5.2)

образуют две пары вертикальных двугранных углов.

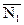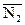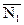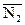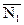Углом между плоскостями будем называть любой из двух смежных двугранных углов. Один из них равен углу j между векторами (A₁, B₁, C₁) и (A₂, B₂, C₂), перпендикулярными соответственно к плоскостям (6.5.1) и (6.5.2), а второй - j₁=180⁰-j. Следовательно искомый угол можно найти по формуле: (, )=ô ôô 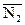ôcosj Þ

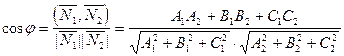(6.5.3)

Если плоскости параллельны, то угол j между ними равен 0 или p, отсюда следует, что 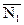и 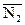коллинеарны и мы получим условие параллельности двух плоскостей

A₁/A₂ = B₁/B₂ = C₁/C₂ (6.5.4)

Еслиj=p¤2, то из формулы (6.5.3) получим условие перпендикулярности двух прямых

A₁A₂ + B₁B₂ + C₁C₂ = 0 (6.5.5)

Замечание: Если выполняется условие A₁/A₂=B₁/B₂=C₁/C₂=D₁/D_2, то плоскости совпадают.