Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых

Пусть даны прямые l₁ и l₂:

(x-x₁)/m₁=(y-y₁)/n₁=(z-z₁)/p₁ (6.9.1)

(x-x₂)/m₂=(y-y₂)/n₂=(z-z₂)/p₂ (6.9.2)

Определение. Углом между двумя прямыми l₁ и l₂ называется угол между их направляющими векторами 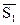(m₁,n₁,p₁) и 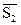(m₂,n₂,p₂) (рис.6.5.).

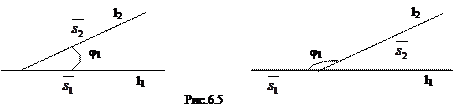
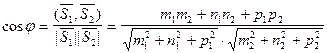(6.9.3)

Если прямые (6.9.1) и (6.9.2) параллельны, то 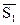и 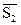коллинеарны. Отсюда получаем условие параллельности прямых:

m₁/m₂ = n₁/n₂ = p₁/p₂ (6.9.4)

Если прямые (6.9.1.)и (6.9.2.) взаимно перпендикулярны, то 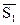и 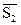также перпендикулярны и их скалярное произведение равно нулю, т.е. (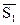 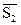) = 0 Þ

m₁m₂ + n₁n₂ + p₁p₂ = 0 (6.9.5.)

Это условие перпендикулярности двух прямых

6.10. Угол между прямой и плоскостью.
Условия параллельности и перпендикулярности
прямой и плоскости

Пусть даны прямые: (x-x₀)/m = (y-y₀)/n = (z-z₀)/p (6.10.1)

и плоскость Ax + By + Cz + D (6.10.2)

Углом между прямой l и плоскостью p называется угол j(0<=j<=p/2), образованный прямой с её проекцией на плоскость (рис.6.6.)

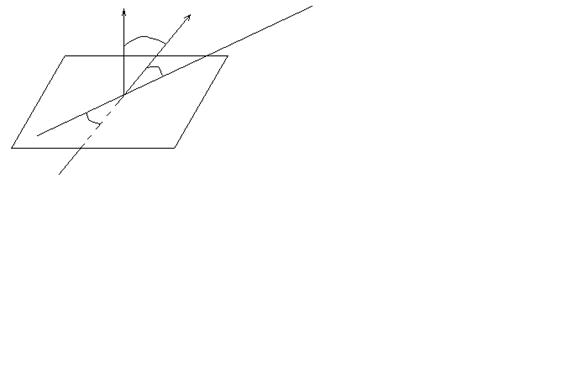
Из рис. 6.6. видно, что угол между 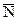(A,B,C) плоскости p и 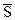(m,n,p) - направляющим вектором прямой равен p/2 - j, поэтому

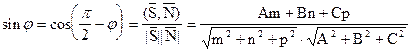(6.10.3)

Условие перпендикулярности прямой (6.10.1) и плоскости (6.10.2) совпадает с условием коллинеарности векторов 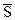и 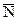, поэтому это условие запишется в виде:

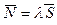или A/m = B/n = C/p (6.10.4)

Условие же параллельности прямой (6.10.1) и плоскости (6.10.2) совпадает с условием перпендикулярности векторов 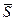и ; следовательно, получим:

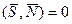или Am + Bn + Cp = 0 (6.10.5)