 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнения прямой, проходящей через две заданные точки
|
|
Пусть прямая проходит через две данные точки М1(x1,y1,z1) и М2(x2,y2,z2). В этом случае можно положить, что направляющий вектор прямой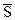 
= 
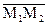(x2 - x1, y2 - y1, z2 - z1)
Подставив в уравнения (6.8.2.4.) m = x2-x1, n = y2 - y1, p = z2 - z1, x0 = x1, y0 = y1, z0 = z1, получим (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) = (z - z1)/(z2 - z1) (6.8.3.1)
Это уравнение прямой, проходящей через две данные точки.
Замечание. 1. Три точки М1,М2,М3 лежат на одной прямой, если выполняется условие (x3 - x1)/(x2 - x1) = (y3 - y1)/(y2 - y1) = (z3 - z1)/(z2 - z1)
2. От общих уравнений прямой (6.8.1.1.) можно перейти к каноническим уравнениям (6.8.2.4) и наоборот.
Дата публикования: 2014-11-04; Прочитано: 414 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
