 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение типовых примеров
|
|
Пример 1. Составить каноническое уравнение эллипса, зная, что большая его ось 2а=10 и эксцентриситет 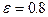 .
.
Решение: По формуле (5.2.4) с= аe =5Ч0.8 = 4, а b находим из равенства b2 = а2 - с2 = 25 - 16 = 9b =3. Подставляя найденные значения а=5, b=3 в уравнение (5.2.2), получим искомое уравнение эллипса 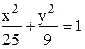
Пример 2. Написать уравнение гиперболы по данной полуоси а = 1 и полуфокусному расстоянию с = 2.
Решение: Из равенства а2 + b2 = с2 найдем полуось b: 1 + b2 = 4 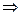 b =
b = 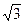 .
.
Искомое уравнение гиперболы будет иметь вид 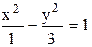
Пример 3. Найти координаты фокуса и уравнение директрисы параболы х = -5у2
Решение: Перепишем уравнение так: 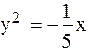 и, сравнивая его с уравнением у2 = -2рх, получим
и, сравнивая его с уравнением у2 = -2рх, получим 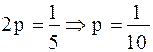 . Координаты фокуса
. Координаты фокуса 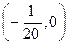 и уравнение директрисы
и уравнение директрисы 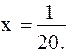
Пример 4. Найти координаты вершины параболы, заданной уравнением х=у2+4у+1. Написать уравнение оси симметрии.
Решение: Найдем координаты вершины параболы: х = (у2 + 4у + 4) - 4 + 1 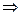 х+3=(у+2)2. Следовательно вершина параболы лежит в точке (-3,-2).
х+3=(у+2)2. Следовательно вершина параболы лежит в точке (-3,-2).
Уравнение оси параболы у = -2.
Пример 5. Найдите координаты точки М до поворота осей, если после поворота их на 1350 точка М имеет координаты (2,-3).
Решение: По формулам (4.2.1) преобразования координат получим:
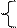 х= 2 cos1350 - (-3) sin1350
х= 2 cos1350 - (-3) sin1350
y= 2 sin1350 +(-3) cos1350 ,
отсюда 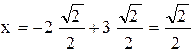 ,
, 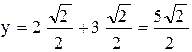 , следовательно, координаты до поворота осей
, следовательно, координаты до поворота осей 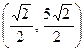 .
.
Дата публикования: 2014-11-04; Прочитано: 347 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
