Решение. За что зацепиться в этой задаче

За что зацепиться в этой задаче.

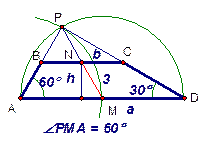
Хорошо бы знать длины сторон, а не длину средней линии. Тогда можно определить высоту трапеции. Попробуем это сделать.

Длины сторон основания 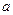и .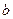

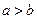
Проведем боковые стороны трапеции до пересечения в точке 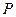. Медианы прямоугольных треугольников равны половине длины гипотенузы.

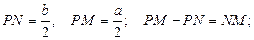
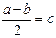
Решаем систему уравнений

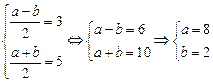
Опять вернемся к вопросу:

как найти площадь трапеции.

Известна формула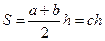

Получается, практически мы не сдвинулись. Не определена высота.

Как еще можно определить площадь трапеции?

Как разность двух площадей треугольников.

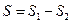
Здесь 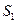и 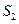– площади прямоугольных треугольников.

Площадь прямоугольного треугольника по заданной гипотенузе и острому углу

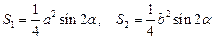
Площадь трапеции .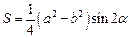

В качестве угла можно принять любой из острых углов

Кстати, можно было не решать приведенную систему

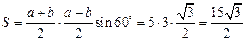
Можно поступить и по-другому.

Так как треугольник 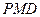– равнобедренный, то угол 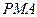равен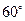

Высота трапеции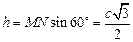

Площадь трапеции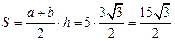

Ответ: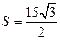

Задача 16.

Средняя линия трапеции равна 4, углы при основании равны 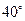и 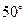. Найдите основания трапеции, если отрезок, соединяющий середины оснований, равен 1.