Решение. Для определения совместности системы воспользуемся теоремой Кронекера-Капелли

Для определения совместности системы воспользуемся теоремой Кронекера-Капелли. Для этого найдем ранг матрицы и ранг расширенной матрицы системы .

Выпишем матрицу системы , столбец свободных членов 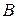и расширенную матрицу :

, , .

Ранг матрицы А не может быть больше 3, но существует минор третьего порядка не равный нулю:

.

Таким образом, . Вычислим ранг расширенной матрицы , ее определитель:

,

т. е. . Ранги матриц и различны, следовательно, исследуемая система несовместна.

Таким образом, можно выделить два основных случая:

1) Если ранг матрицы системы r равен числу уравнений n, то система имеет единственное решение;

2) Если ранг матрицы системы r меньше числа неизвестных n и система совместна, то система имеет бесконечное множество решений. В этом случае (n - r) неизвестных могут быть выбраны произвольно, а оставшиеся r неизвестных определятся единственным образом.

8. Решение систем линейных уравнений

методами линейной алгебры