Решение. Найдем определитель матрицы :

Найдем определитель матрицы :

,

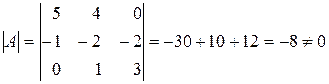т.е. матрица является невырожденной.

Найдем алгебраические дополнения:

,	,	,
,	,	,
,	,	.

.

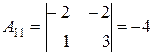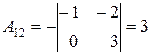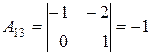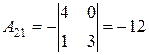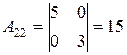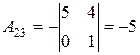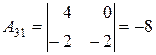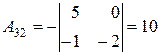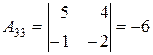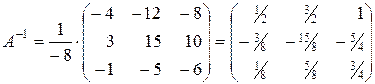Сделаем проверку:

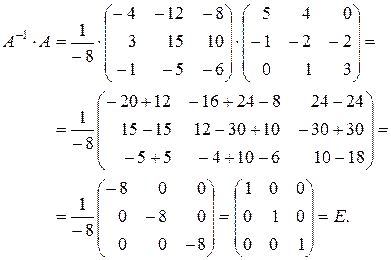
Следовательно, матрица 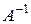найдена верно.

7. Вопросы существования решения систем

линейных уравнений

Рассмотрим систему линейных уравнений

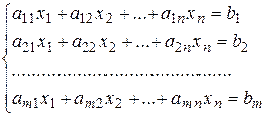, (3)

где – неизвестные ;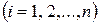

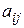– коэффициенты системы ;

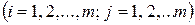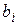– свободные члены .

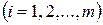Система (3) может быть записана в матричной форме:

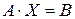, (4)

где – матрица коэффициентов при неизвестных,

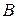– столбец свободных членов,

– столбец переменных, т.е.

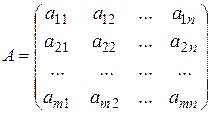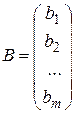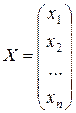, , . (5)

Решением системы называется любое множество чисел

, , …, ,

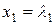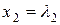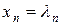которые обращают все уравнения системы в тождества.

Система, имеющая хотя бы одно решение, называется совместной. Совместная система может иметь одно или несколько решений.

Например, система

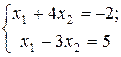
совместна и имеет единственное решение 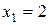, 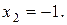(Проверьте подстановкой значений в систему).

Система

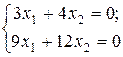
совместна, но имеет бесконечное множество решений: 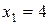, 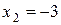; 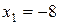, 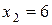; и т.д.

Система, не имеющая решения, называется несовместной.

Система, имеющая единственное решение, называется определенной.

Система, имеющая несколько решений, называется неопределенной.