Ранг матрицы. Рангом матрицы называется наибольший порядок миноров, отличных от нуля

Рангом матрицы называется наибольший порядок миноров, отличных от нуля. Т.е. матрица имеет ранг , если среди ее миноров существует хотя бы один минор порядка , отличный от нуля, а все миноры порядка 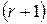и выше равны нулю или не существуют.

Ранг нулевой матрицы считается равным нулю.

Если матрица – квадратная, порядка , то ее ранг .

Если матрица имеет размер , то ее ранг будет не больше наименьшего из чисел и , т.е. .

Пример 5.1. Найти ранг матрицы .

Решение. Матрица имеет порядок , следовательно, ее ранг не может быть больше 3. Посчитаем определитель третьего порядка:

,

он равен нулю. Это означает, что ранг матрицы будет меньше 3. Но существует минор второго порядка, отличный от нуля

,

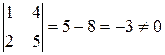т.е. ранг матрицы .

Пример 5.2. Найти ранг матрицы .

Решение.

Имеем матрицу размерности и, следовательно, ее ранг не больше 3 (наименьшее из чисел 3 и 5).

Существует определитель третьего порядка

,

он равен нулю. Несмотря на это, мы не можем сделать какой-то вывод о ранге матрицы , т. к. есть другие миноры третьего порядка. Возьмем, например, такой минор:

.

Он отличен от нуля, поэтому ранг матрицы равен 3.