Решение систем линейных уравнение методом Крамера

Рассмотрим случай, когда число уравнений системы равно числу неизвестных. Тогда система (3) примет вид:

. (6)

Определитель матрицы называют основным определителем системы и записывают так:

. (7)

Выпишем вспомогательные определители , соответствующие каждой переменной 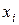, которые получаются путем замены -го столбца основного определителя столбцом свободных членов :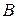

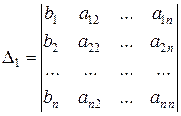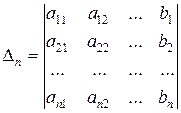, ,…, . (8)

Проанализировав из (7) и из (8) о решении системы (6) можно сказать следующее:

§ если , то система имеет единственное решение;

§ если , а среди определителей имеются не равные нулю, то система не имеет решений. Отсутствие решений обусловливается тем, что одно из уравнений противоречит остальным.

§ если и все , то система имеет бесконечное множество решений. Это обусловлено тем, что одно из уравнений является следствием других.

Для решения системы методом Крамера необходима невырожденность матрицы , т.е. ее определитель не должен быть равен нулю, а это говорит о том, что система (6) в этом случае будет иметь единственное решение и оно может быть представлено в таком виде:

, , …, ,

где и – определители из (7) и (8).

Пример 7.2. Имеет ли данная система решение?

Решение.

Легко проверить, что . Таким образом, можно сделать вывод, что система имеет бесконечное множество решений. Это обусловлено тем, что третье уравнение системы является суммой первых двух.

Пример 7.3. Решить систему методом Крамера

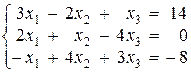
Решение. Выпишем матрицы и :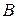

, .

, ,

, .

Решение системы следующее:

, , .

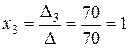Проверка показала, что , , 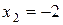удовлетворяют уравнениям данной системы, следовательно, являются ее решением.