 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства определителей. 1о Если в определителе поменять местами строки и столбцы, то его значение не изменится
|
|
1о Если в определителе поменять местами строки и столбцы, то его значение не изменится. То есть значение определителя матрицы  равно значению определителя матрицы
равно значению определителя матрицы  , транспонированной по отношению к матрице
, транспонированной по отношению к матрице  .
.
Например,  .
.
Это свойство устанавливает равноправие строк и столбцов.
2о Если в определителе поменять местами две строки (столбца), то его знак изменится на противоположный.
Например, 
| – здесь поменяли местами первый и второй столбцы. |
3о Если в определителе элементы какой-либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Например, 
| – здесь элементы третьего столбца исходного определи-теля имеют общий множитель 2. |
Замечание. Обратите внимание на то, что если умножаем матрицу на число, то умножаются все ее элементы на это число, а для того, чтобы умножить определитель на число – достаточно на это число умножить элементы какой либо одной строки (столбца).
4о Если в определителе какую-либо строку (столбец) умножить на некоторое число и сложить с другой строкой (столбцом), то его значение не изменится.
Например, 
| – здесь первый столбец сложили со вторым, умножен-ным на 3. |
5о Если каждый элемент  -го столбца (строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых первый в
-го столбца (строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых первый в  -том столбце (строке) имеет первые из упомянутых слагаемых, а другой – вторые; элементы, стоящие на остальных местах те же, т.е.
-том столбце (строке) имеет первые из упомянутых слагаемых, а другой – вторые; элементы, стоящие на остальных местах те же, т.е.
 .
.
Например, 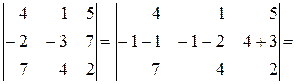 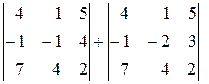
|
6о Определитель равен нулю, если:
§ он имеет два одинаковых столбца (или строки);
§ все элементы некоторого столбца (или строки) равны нулю;
§ соответствующие элементы двух его строк (или столбцов) пропорциональны;
§ одна из его строк (столбцов) есть линейная комбинация двух других его строк (столбцов).
Таким образом,
 ;
;  ;
;  ;
; 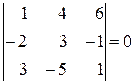 .
.
В первом определителе первая и третья строки одинаковые; во втором – вторая строка состоит из нулей; в третьем – третья строка есть первая, умноженная на (–2); в четвертом – третий столбец есть первый, умноженный на 2 плюс второй, т.е. третий столбец – это линейная комбинация первых двух.
Дата публикования: 2014-11-04; Прочитано: 2341 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
