Решение. Решение можно разбить на этапы

Решение можно разбить на этапы.

Первый этап. Внесем в таблицу элементы матрицы , столбца В и подсчитаем сумму элементов по строкам, записав эти числа в контрольный столбец К:

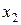
				К
	– 2
		– 4		– 1
– 1			-8	– 2

Второй этап. Первую строку оставляем без изменения. Элемент, стоящий в верхнем левом углу, назовем главным, остальные элементы первого столбца заменяем нулями. Оставшиеся элементы находим по правилу “прямоугольника”:

§ искомый и главный элементы являются вершинами прямоугольника, остальные две его вершины определяем единственным образом;

§ находим разность произведений первых двух вершин и вторых.

Таким образом, таблица приобретет вид:

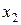
				К
	– 2
		– 14	– 28	– 35
			– 10

Проверьте, что числа контрольного столбца, найденные по правилу “прямоугольника”, являются суммами по строкам. Заметим, что вторая строка кратна 7, а третья – 10. Для простоты вычислений, разделим строки на эти числа:

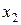
				К
	– 2
		– 2	– 4	– 5
			– 1

Третий этап. Первую и вторую строки оставляем без изменения. На этом этапе главным элементом является второй элемент главной диагонали. Элемент, стоящий под ним заменяем нулем, оставшиеся элементы вновь находим по методу “прямоугольника”. Таким образом, таблица приобретет вид:

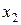
				К
	– 2
		– 2	– 4	– 5

Третья строка кратна 3, разделим все ее элементы на это число:

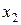
				К
	– 2
		– 2	– 4	– 5

Итак, мы привели систему к треугольному виду, а именно:

.

Подставим во второе уравнение системы 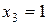и найдем ; при подстановке в первое уравнение системы, получаем . Решение системы может быть записано в виде:

.

Решение системы методом Гаусса можно проводить в несколько иной форме. Рассмотрим его на следующем примере:

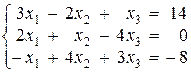
Первый этап. Первое уравнение системы оставим без изменений, а из второго и третьего уравнений исключим :

Второй этап. Первое и второе уравнение системы оставляем без изменений. Из третьего уравнения исключаем переменную :

Третий этап. Подставим во второе уравнение системы 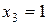и найдем ; при подстановке в первое уравнение системы, получаем . Решение системы может быть записано в виде:

.

Естественно, что решения исходной системы, найденные методами Крамера, обратной матрицы и методом Гаусса совпадают.

iI. в Е К Т О Р Ы

Основные понятия

Вектором называется направленный отрезок , в котором точка рассматривается как начало, а точка 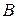– как его конец.

Проекцией вектора на ось называется длина вектора , где и – проекции точек и 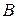на ось (основания перпендикуляров, проведенных из точек и 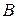на ось ):

.

Проекция вектора на ось равна его модулю, умноженному на косинус угла наклона вектора к этой оси:

,

где - угол наклона вектора к оси .

Замечание. Если направление вектора совпадает с направлением оси, то берем полученное значение со знаком “+”, в противоположном случае – со знаком “–”.

Координатамивектора называются проекции этого вектора на оси координат:

, ,

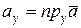и записываются:

или .

Координаты вектора равны разностям соответствующих координат его конца и начала , т.е.

.

Длиной (модулем) вектора называется длина отрезка 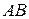и обозначается . Длина (модуль) вектора равна корню квадратному из суммы квадратов его координат:

.

Коллинеарными называются два параллельных или лежащих на одной прямой вектора. Векторы коллинеарны тогда и только тогда, когда их координаты пропорциональны, т.е. векторы и коллинеарны, если выполняется соотношение:

.

Нулевым вектором называется вектор, длина которого равна нулю. Этот вектор считается коллинеарным любому вектору.

Единичным вектором (ортом) называется вектор, длина которого равна единице.

Компланарными называются три вектора и более векторов, если они, будучи приведены к общему началу, лежат в одной плоскости.

Равными называются два коллинеарных вектора, имеющих одинаковые направления и одинаковые длины.

Противоположными называются два коллинеарных вектора одинаковой длины и противоположных по направлению. Вектор, противоположный вектору – есть вектор (), т.е.

, .

Пример 1.1. При каком значении векторы и будут коллинеарными?

Решение. Для того, чтобы векторы были коллинеарными, необходимо, чтобы их координаты были пропорциональны, т.е.

.

Подставим координаты векторов в это соотношение:

,

тогда

.

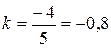Пример 1.2. Даны точки 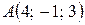, . Найти проекцию вектора на ось , если известно, что вектор и ось образуют между собой угол в .

Решение.

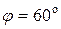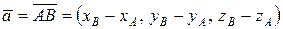. В нашем случае , . Найдем координаты вектора . По формуле , получим, что

.

Определим длину вектора:

.

Итак,

.

2. Линейные операции над векторами

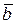Суммой двух векторов и называется вектор , который идет из начала вектора в конец вектора 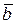, при условии, что начало вектора 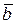приложено к концу вектора . При сложении векторов их координаты складываются, т.е. если , , то

.

Суммой векторов называется вектор , идущий из начала вектора в конец вектора , при условии, что начало вектора приложено к концу вектора , начало вектора – к концу вектора , и т.д. пока не дойдет до вектора .

Если , ,…, , то

.

Замечание. Если конец вектора совпадает с началом вектора , то сумма и вектор является нулевым.

Разностью векторов 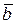и называется вектор , который в сумме с вектором составляет вектор .

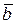Разностью двух векторов, приведенных к общему началу, является вектор, идущий из конца “вычитаемого” вектора в конец “уменьшаемого”.

При вычитании векторов их координаты вычитаются, т.е. если , , то

.

Произведениемвектора на число называется вектор, который коллинеарен вектору , имеет длину , и направление такое же как у вектора , если , и противоположное, если . При умножении вектора на число координаты вектора умножаются на это число, т.е.

.

Свойства линейных операций над векторами

1^о .

2^о .

3^о .

4^о .

5^о .

6^о .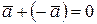

7^о .