 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема Кронекера-Капелли. Припишем к матрице столбец свободных членов , тогда образованная матрица
|
|
Припишем к матрице 
столбец свободных членов 
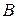, тогда образованная матрица
является расширенной матрицей системы (3).
| Теорема Кронекера-Капелли | Для того, чтобы система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы. |
Пример 7.1.
Определить, совместна ли система
Дата публикования: 2014-11-04; Прочитано: 527 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
