 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение систем линейных уравнений методом обратной матрицы
|
|
Для решения системы (6) этим методом также необходима невырожденность матрицы  . В таком случае будет существовать матрица
. В таком случае будет существовать матрица 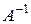 , обратная к матрице
, обратная к матрице  .
.
Умножим соотношение (4) на 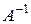 , тогда
, тогда
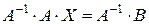 ,
,
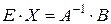 .
.
Таким образом,
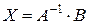 . (9)
. (9)
Для того, чтобы найти решение системы методом обратной матрицы, необходимо:
1) проверить невырожденность матрицы  ;
;
2) найти 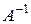 по формуле (1);
по формуле (1);
3) вычислить значения неизвестных по формуле (9).
Пример 7.4 Решить систему методом обратной матрицы
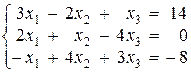
Выпишем матрицы  ,
, 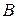 и
и  :
:
 ,
,  ,
,  .
.
1) Проверим невырожденность матрицы  :
:
 .
.
2) Найдем 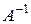 , для этого выпишем алгебраические дополнения матрицы
, для этого выпишем алгебраические дополнения матрицы  :
:
 , ,
| 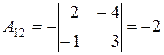 , ,
|  , ,
| ||||
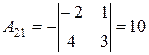 , ,
|  , ,
| 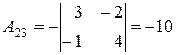 , ,
| ||||
 , ,
|  , ,
|  . .
| ||||
Тогда
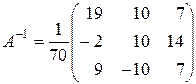 .
.
3) Решение системы найдем из равенства 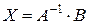 :
:
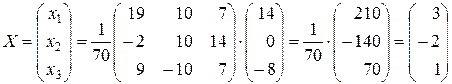 .
.
Итак,
 ,
,  ,
, 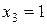 .
.
Дата публикования: 2014-11-04; Прочитано: 605 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
