 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Обратная матрица. ► Определение. Квадратная матрица называется невырожденной, если ее определитель не равен нулю
|
|
► Определение. Квадратная матрица  называется невырожденной, если ее определитель не равен нулю
называется невырожденной, если ее определитель не равен нулю 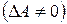 . В противном случае она будет вырожденной.
. В противном случае она будет вырожденной.
► Определение. Матрица 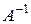 называется обратной квадратной матрице
называется обратной квадратной матрице  , если
, если 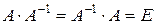 , где
, где 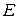 – единичная матрица.
– единичная матрица.
Теорема. Всякая невырожденная матрица имеет обратную.
Для матрицы
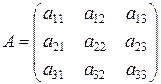
обратная матрица 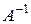 равна транспонированной матрице алгебраических дополнений, деленных на определитель матрицы, т.е. имеет вид:
равна транспонированной матрице алгебраических дополнений, деленных на определитель матрицы, т.е. имеет вид:
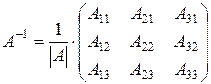 , (1)
, (1)
где 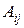 – алгебраические дополнения к элементам матрицы
– алгебраические дополнения к элементам матрицы  , т.е.
, т.е.
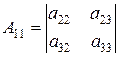 , ,
| 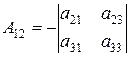 , ,
| 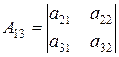 , ,
| (2) |
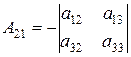 , ,
|  , ,
| 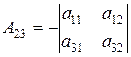 , ,
| |
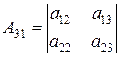 , ,
| 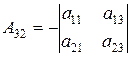 , ,
| 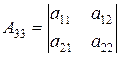 . .
|
Чтобы найти обратную матрицу 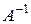 к матрице
к матрице  , необходимо:
, необходимо:
§ вычислить определитель матрицы  (он не должен равняться нулю);
(он не должен равняться нулю);
§ найти алгебраические дополнения ко всем элементам матрицы  (по формулам (2);
(по формулам (2);
§ записать обратную матрицу по формуле (1);
§ сделать проверку, т.е. перемножить матрицы  и
и 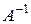 , в результате чего должна получиться единичная матрица
, в результате чего должна получиться единичная матрица 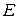 .
.
Пример 6.1. Найти матрицу, обратную данной матрице
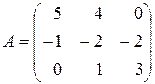 .
.
Дата публикования: 2014-11-04; Прочитано: 739 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
