Разложение векторов по базису

Пусть - векторы пространства R; - скаляры, тогда вектор называется линейной комбинацией векторов .

Если вектор равен нулю тогда и только тогда, когда все числа , то говорят, что векторы линейно независимы.

Если вектор равен нулю и среди чисел есть хотя бы одно, отличное от нуля, то говорят, что векторы линейно зависимы.

Теорема 1.

Если векторы , принадлежащие пространству R, линейно зависимы, то по крайней мере, хотя бы один из них является линейной комбинацией остальных.

Пространство R называется n -мерным, если в нем существует n линейно независимых векторов и не существует большего числа линейно независимых векторов.

Совокупность n линейно независимых векторов n мерного пространства R называется базисом этого пространства.

Если нам задана в трехмерном пространстве система декартовых прямоугольных координат, то вместе с нею мы будем рассматривать тройку векторов, которую обозначим символами 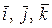. Эти векторы определяются следующими условиями:

1) вектор лежит на оси , вектор – на оси 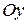, вектор – на оси ;

2) каждый из векторов 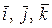направлен на своей оси в положительную сторону;

3) векторы 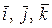- единичные, т.е. .

Любой вектор в пространстве может быть выражен через 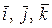при помощи линейных операций. Представление вектора в виде суммы 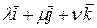называется разложением вектора по базису 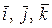. Числа называются коэффициентами этого разложения; векторы 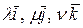называются составляющими (или компонентами) вектора по базису .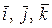

Теорема 2.

Каким бы ни был вектор , он всегда может быть разложен по базису 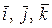, т.е. может быть представлен в виде Коэффициенты этого разложения определяются как проекции вектора на координатные оси, т.е. , , .

Замечание. Разложение векторов можно производить не только по базису .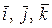

Замечание. Три вектора , , могут являться базисом пространства , если определитель, составленный из координат этих векторов будет не равным нулю, т.е.

.

Теорема 3.

Каким бы ни был вектор , он всегда может быть выражен в виде линейной комбинации векторов , т.е. . Такое выражение вектора называется разложением его по базису .

Например, если требуется разложить вектор 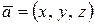по базису , , , т.е. представить в виде: , следует выполнить такие действия:

1) проверить, действительно ли векторы образуют базис в пространстве , т.е.

;

2) Найти из системы

3) Представить в виде (в базисе вектор будет иметь координаты ).

Пример 2.1. Показать, что векторы , , образуют трехмерный базис и найти координаты вектора в этом базисе.

Решение.

1) .

Определитель не равен нулю, т.е. векторы образуют трехмерный базис.

2) Для вычисления координат вектора в этом базисе составим систему линейных уравнений:

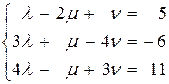
Отсюда,

, , .

3) Таким образом, . То есть вектор в базисе имеет координаты: .