Условия потенциальности поля

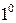. Циркуляция векторного поля по любому замкнутому контуру, лежащему в области непрерывности потенциального поля, равна нулю.

Доказательство:

Рассмотрим

+

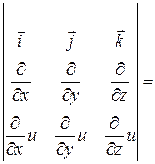
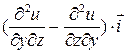
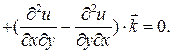
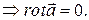
По теореме Стокса = .

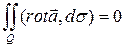. Линейный интеграл в потенциальном поле не зависит от пути интегрирования и равен разности потенциалов поля в конечной и начальной точках интегрирования.

Доказательство:

Так как поле потенциально ,

= = =

= + = =

-

- .

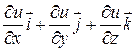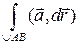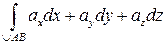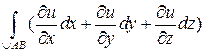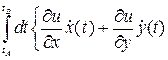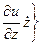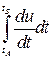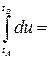
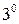. Для того чтобы векторное поле 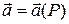в некоторой односвязной области

G было потенциальным, необходимо и достаточно, чтобы оно было

безвихревым, т.е. .

Доказательство:

Необходимость

Пусть 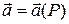- потенциальное поле .

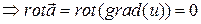Достаточность

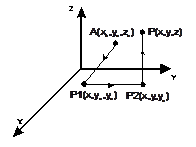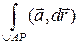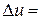
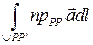
В силу условия ,если зафиксировать начальную точку А (0,0,0), криволинейный интеграл станет некоторой функцией переменной точки P (x,y,z): u (P) = . Вычислим производную функции u (P) в точке A. При переходе от точки P к точке P ' функция u получит приращени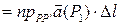е = , где 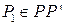по теореме о среднем. Следовательно, . Переходя к пределу при и , имеем 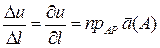. Поскольку производная поля по направлению AP равняется проекции grad (u) на это направление, то .

Данное условие 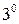используется в качестве критерия потенциальности векторного поля.