 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Формула Грина
|
|
Пусть в односвязной плоской области D, имеющей границу L, задано непрерывно дифференцируемое векторное поле 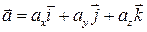 , тогда
, тогда 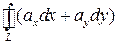 =
= 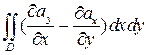 , при этом контур обходится так, чтобы область D оставалась слева.
, при этом контур обходится так, чтобы область D оставалась слева.
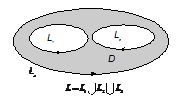 Доказательство:
Доказательство:
Рассмотрим формулу Стокса для данного случая:
 =
= 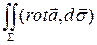 .
.
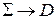 :
: 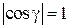 ,
, 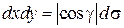 ;
; 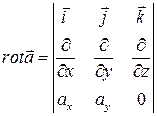 ; откуда следует
; откуда следует 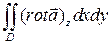 =
= 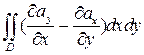 .
.
Область D может быть и неодносвязной. В этом случае под линейным интегралом понимается сумма по всем компонентам границы D.
В некоторых случаях формула Грина позволяет упростить вычисление циркуляции векторного поля.
ПРИМЕР  . Вычислите циркуляцию вектора
. Вычислите циркуляцию вектора
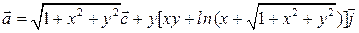
по контуру L: x 2 + y 2 = R 2.
Тогда: C = 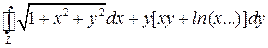 .
.
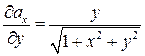
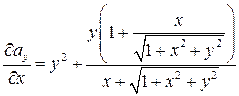 =
=
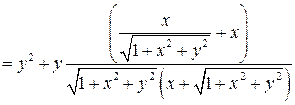 =
= 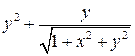 .
.
С = 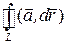 =
= 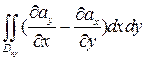 =
= 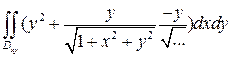 =
=
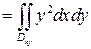 =
= 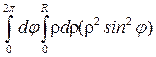 =
=
= 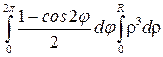 =
=
= 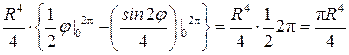 .
.
Дата публикования: 2014-11-04; Прочитано: 419 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
