 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Оператор Лапласа
|
|
Дифференциальные операции второго порядка возникают в результате двукратного применения к полям оператора «набла».
Если в области G задано скалярное поле  , то операция взятия градиента порождает векторное поле:
, то операция взятия градиента порождает векторное поле: 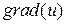 . В векторном поле
. В векторном поле 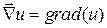 операция взятия дивергенции порождает скалярное поле:
операция взятия дивергенции порождает скалярное поле:  , а операция взятия ротора - векторное поле
, а операция взятия ротора - векторное поле 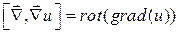 .
.
Если в области G задано векторное поле 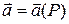 , то операция взятия дивергенции порождает скалярное поле:
, то операция взятия дивергенции порождает скалярное поле: 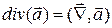 . В скалярном поле
. В скалярном поле 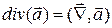 операция взятия градиента порождает векторное поле:
операция взятия градиента порождает векторное поле: 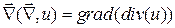 .
.
Если в области G задано векторное поле 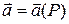 , то операция взятия ротора порождает векторное поле
, то операция взятия ротора порождает векторное поле 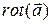 . Применяя повторно к этому полю оператор
. Применяя повторно к этому полю оператор 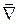 , получим скалярное поле
, получим скалярное поле  и векторное поле
и векторное поле  .
.
При помощи оператора Гамильтона основные понятия теории поля можно записать в виде операций векторной алгебры.
Рассмотрим некоторые операции второго порядка
1. Вихревое поле является соленоидальным: 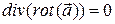 .
.
Раскроем смешанное произведение, учитывая, что векторное произведение одинаковых векторов равно нулю: 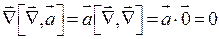 .
.
2. Векторное поле 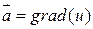 является безвихревым, так как
является безвихревым, так как 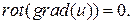 Действительно,
Действительно, 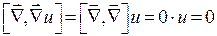 .
.
3. Рассмотрим операцию 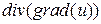 .
.

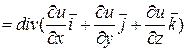 =
=  .
.
ОПРЕДЕЛЕНИЕ. Дифференциальный оператор вида  называется оператором Лапласа. Оператор Лапласа можно представить как скалярное произведение оператора Гамильтона самого на себя:
называется оператором Лапласа. Оператор Лапласа можно представить как скалярное произведение оператора Гамильтона самого на себя:
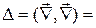 =
=  .
.
Уравнение вида  называется уравнением Лапласа и является одним из основных уравнений математической физики. Непрерывное решение уравнения Лапласа u (x, y, z) называется гармонической функцией. Соответствующее скалярное поле называется гармоническим или лапласовым.
называется уравнением Лапласа и является одним из основных уравнений математической физики. Непрерывное решение уравнения Лапласа u (x, y, z) называется гармонической функцией. Соответствующее скалярное поле называется гармоническим или лапласовым.
Векторное поле является гармоническим, если оно является одновременно потенциальным и соленоидальным: 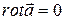 ;
; 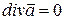 .
.
Рассмотрим операцию 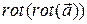 .
.
Формула двойного векторного произведения дает: 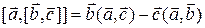 {формула «бац минус цаб»}. Тогда
{формула «бац минус цаб»}. Тогда 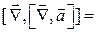
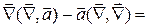
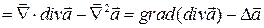 .
.
Дифференциальные операции второго порядка удобно свести в таблицу.
| Скалярное поле | Векторное поле | ||
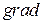
| 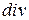
| 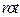
| |
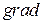
| 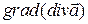
| ||
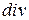
| 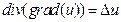
| 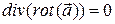
| |
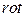
| 
| 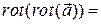
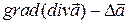
|
Например, законы электромагнетизма описываются уравнениями Максвелла в дифференциальной форме:
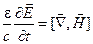 ;
; 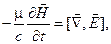 ;
; 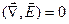 ;
; 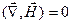 .
.
Иначе:
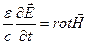 (1),
(1),
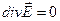 (2);
(2);
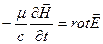 (3),
(3),
 (4).
(4).
В данном случае нет зарядов и токов, а 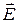 ,
,  - векторы напряжённости электрического и магнитного полей;
- векторы напряжённости электрического и магнитного полей; 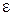 ,
, 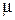 - электрическая и магнитная проницаемость; c - скорость света.
- электрическая и магнитная проницаемость; c - скорость света.
Если продифференцировать (1) по 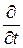 и подставить
и подставить 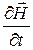 из (3), то получим
из (3), то получим
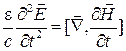 или
или 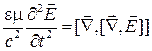 .
.
Преобразуем правую часть по формуле: 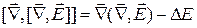 .
.
Итак, для векторного поля 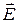 имеем уравнение
имеем уравнение 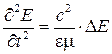 .
.
Это одно из основных уравнений математической физики, называемое волновым уравнением.
Дата публикования: 2014-11-04; Прочитано: 614 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
