 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Корни уравнения четвертой степени
|
|
Уравнение четвертой степени
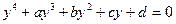 (2.4) решается методом Феррари. Преобразуем левую часть (2.4) с помощью вспомогательного параметра
(2.4) решается методом Феррари. Преобразуем левую часть (2.4) с помощью вспомогательного параметра  следующим образом:
следующим образом:

 . (2.5) Параметр
. (2.5) Параметр  подбирается таким образом, чтобы выражение, стоящее во вторых скобках правой части, было квадратом двучлена первой степени.
подбирается таким образом, чтобы выражение, стоящее во вторых скобках правой части, было квадратом двучлена первой степени.
Следовательно, должно выполняться условие 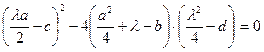 .
.
Это уравнение третьей степени относительно  , которое решается по формулам Кардана. Пусть
, которое решается по формулам Кардана. Пусть  − один из корней этого уравнения. Тогда выражение
− один из корней этого уравнения. Тогда выражение  приводится к виду:
приводится к виду:
 ,
,
где  ,
,  , а уравнение (2.4) принимает вид
, а уравнение (2.4) принимает вид
 или
или
 .
.
Решение последнего уравнения сводится к решению двух квадратных уравнений.
П р и м е р. Решить уравнение  .
.
Решение. Введем дополнительный параметр  и преобразуем левую часть исходного уравнения:
и преобразуем левую часть исходного уравнения:

 .
.
Рассмотрим уравнение  . Это уравнение имеет один кратный корень, если
. Это уравнение имеет один кратный корень, если  , т. е. выполняется равенство
, т. е. выполняется равенство
 .
.
При решении этого уравнения получаем, что один из его корней  . При этом значении
. При этом значении  уравнение принимает вид
уравнение принимает вид
 , т. е.
, т. е.  .
.
Из полученных соотношений находим корни исходного уравнения:  ,
, 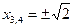 .
.
Дата публикования: 2015-11-01; Прочитано: 451 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
