Тригонометрическая форма комплексного числа

Введем на комплексной плоскости Оху полярную систему координат так, чтобы полюс находился в начале О прямоугольной системы, а полярная ось совпадала с положительной полуосью Ох.

Рассмотрим комплексное число . По формулам, связывающим прямоугольные и полярные координаты, получим тригонометрическую запись комплексного числа :

. (1.4)

Число называется модулем, а число − аргументом комплексного числа , они обозначаются соответственно и . Аргумент числа z определен не однозначно, а с точностью до слагаемого 2pп, где п = 0, ± 1, ± 2,… Модуль r числа z имеет значение . Значение аргумента, удовлетворяющее неравенствам , называется главным значением аргумента и обозначается j = arg z.

Аргумент комплексного числа z = 0 не определен, а его модуль равен нулю.

П р и м е р. Представить в тригонометрической форме число .

Решение. По формулам для нахождения модуля и аргумента комплексного числа , , . Следовательно, аргумент находится во второй четверти и равен . Искомая тригонометрическая форма имеет вид .

В тригонометрической форме удобно выполнять действия умножения и деления комплексных чисел.

Теорема. Модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов множителей:

, . (1.5)

Модуль отношения комплексных чисел 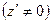равен отношению модулей, а аргумент – разности аргументов множителей:

, . (1.6)

Доказательство. Пусть числа 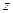и записаны в тригонометрической форме, т. е. и . Непосредственным умножением получаем:

.

При помощи известных тригонометрических формул это соотношение позволяет записать в тригонометрической форме число :

.

Если , то . Поэтому , . Следовательно, , . Теорема доказана.