Свойства взаимно простых многочленов

1. Если произведение делится на и , то 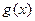делится на .

Доказательство. Так как , то найдутся многочлены и такие, что . Умножим это равенство на 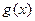, получим, что . Оба слагаемых в правой части делятся на (первое потому, что по условию делится на ). Следовательно, 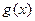делится на .

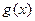2. Если и взаимно просты с , то произведение взаимно просто с .

Доказательство. Многочлены и взаимно просты с , следовательно, существуют многочлены и такие, что . Умножим обе части равенства на 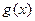. Получим . Делитель и является также делителем 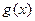. Однако 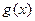и взаимно простые, следовательно, произведение взаимно просто с .

3. Если многочлены и взаимно просты, многочлен делится на каждый из них, то делится на произведение .

Доказательство. Многочлен делится на , поэтому существует многочлен такой, что . многочлен делится на , следовательно, произведение делится на . Многочлены и взаимно просты, поэтому делится на , т. е. существует многочлен такой, что и , ч. и т. д.

Определение. НОД многочленов , ,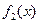…, , равен наибольшему общему делителю многочлена и многочленов ,…, .

Определение. Система многочленов называется взаимно простой, если наибольшими общими делителями этих многочленов являются лишь многочлены нулевой степени.

Замечание. Если 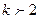, то многочлены попарно могут не быть взаимно простыми: , ,