 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Извлечение квадратного корня из комплексного числа
|
|
Извлечение корня из комплексного числа можно осуществить, не обращаясь к тригонометрической форме. Выведем алгебраическую формулу для выполнения этого действия.
Пусть 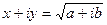 . Интересен случай
. Интересен случай 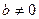 , поэтому рассмотрим только его. Тогда
, поэтому рассмотрим только его. Тогда 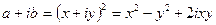 . Это равносильно системе уравнений:
. Это равносильно системе уравнений:
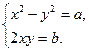 (1.12)
(1.12)
Эта задача имеет вещественные решения, так как всегда существует квадратный корень из комплексного числа. Из второго уравнения системы 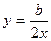 , подставляя которое в первое уравнение системы (1.12), получаем биквадратное уравнение относительно неизвестного
, подставляя которое в первое уравнение системы (1.12), получаем биквадратное уравнение относительно неизвестного 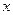 . Его решениями являются
. Его решениями являются 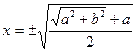 , поэтому
, поэтому 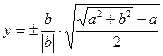 . Для любого вещественного числа t существует функция
. Для любого вещественного числа t существует функция 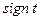 , которая задается следующим образом:
, которая задается следующим образом:
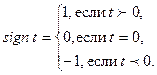 (1.13)
(1.13)
С учетом введенной функции получаем формулу для нахождения квадратного корня из комплексного числа:
 . (1.14)
. (1.14)
П р и м е р. Найти корни уравнения 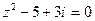 .
.
Решение. Корни уравнения 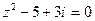 равны
равны 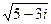 . Пусть
. Пусть 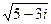 =
= 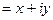 . Относительно неизвестных
. Относительно неизвестных 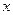 и
и 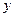 имеем систему уравнений
имеем систему уравнений
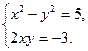
Из второго уравнения этой системы 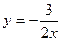 , поэтому относительно неизвестного
, поэтому относительно неизвестного 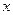 получаем уравнение
получаем уравнение 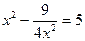 , или
, или 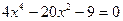 . Учитывая, что
. Учитывая, что 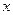 - вещественное число, находим
- вещественное число, находим 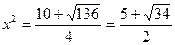 , т. е.
, т. е. 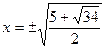 . Следовательно,
. Следовательно, 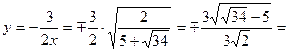
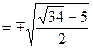 . Таким образом,
. Таким образом, 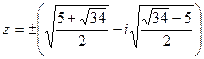 .
.
Дата публикования: 2015-11-01; Прочитано: 676 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
