Извлечение корня из комплексного числа

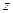Пусть n – натуральное число. Извлечение корня с показателем n из комплексного числа z равносильно нахождению такого комплексного числа w, что . Каждое число w такое, что , называется корнем n-й степени из z и обозначается . Если , то единственным значением является число 0. Рассмотрим случай . Запишем число в тригонометрической форме 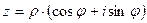и будем искать тоже в тригонометрической форме . Равенство в этом случае запишется в виде

. (1.10)

Учитывая определение равенства комплексных чисел, получим, что у равных комплексных чисел равны модули, а аргументы отличаются на число 2pk, где k Î Z. Таким образом, из формулы (1.10) следует, что , , . Данное число r положительно (так как ) и искомое число должно быть тоже положительным. Известно, что 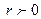такое, что , которое называется арифметическим значение корня n-й степени, и это значение принято записывать в виде степени с дробным показателем, т. е. . Аргумент q находится по формуле . Таким образом, корни n-й степени из комплексного числа z существуют, и все они определяются формулой

, , . (1.11)

Теорема. Существует ровно n значений корня n -й степени из отличного от нуля комплексного числа 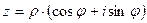, определяемых по формуле , где k = 0, 1, 2,…, n -1.

Доказательство. Существование корней n-й степени из отличного от нуля комплексного числа 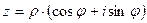было рассмотрено ранее. Аргументы (k = 0, 1, 2,…, n -1) равны 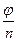, , 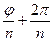, …, идут в возрастающем порядке (т. к. ), причем каждый из них меньше 2p (наибольший из них , так как главное значение аргумента меньше 2p). В пределах одной окружности два различных угла не могут иметь одновременно одинаковые значения синуса и косинуса, следовательно, все значения корней будет различны. Все натуральные числа, большие (п −1), могут быть представлены в виде пт + р, где т и р – натуральные числа, причем р < п. Тогда

= = ,

= = .

Таким образом, значения аргументов совпадают с найденными ранее, т. е. формула (1.11) при условии k = 0, 1, 2,…, n−1 определяет все n различных корней из комплексного числа.

П р и м е р. Найти .

Решение. В тригонометрической форме . Согласно формуле = = + + + . При k = 0, 1, 2 получим три значения корней: 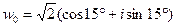, , 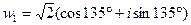. Учитывая, что , получим 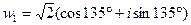= = . Для вычисления и найдем и : , . Поэтому , .