Свойства делимости многочленов

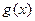1. Если делится на , а 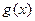делится на , то делится на .

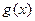Доказательство. Так как делится на , а 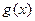делится на , то существуют многочлены и такие, что 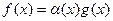и . Поэтому , т. е. делится на .

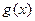2. Если и делятся на , то делится на . Доказать аналогично доказательству свойства 1.

3. Если делится на , то 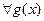произведение делится на . Это свойство предлагается доказать самостоятельно.

4. Если , делится на , то , сумма делится на . Это свойство предлагается доказать самостоятельно.

5. Любой многочлен делится на многочлен нулевой степени.

Доказательство. Пусть С, С ¹ 0 – многочлен нулевой степени. Тогда 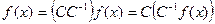, т. е. делится на С.

6. Если делится на , то делится на , где . Это свойство предлагается доказать самостоятельно.

7. Если , − делители многочлена , то они имеют такую же степень, что и .

Доказательство. Многочлен можно представить в виде . Из того, что , следует доказываемое утверждение.

8. Многочлены и 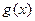делятся друг на друга, если существует , такое, что . Это свойство предлагается доказать самостоятельно.

9. Если , то делитель одного из многочленов и будет делителем и другого многочлена.

Доказательство. Пусть многочлен 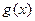является делителем . Тогда существует многочлен такой, что 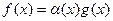. Поэтому , т. е. 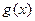является делителем . Если же 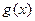является делителем , то существует многочлен такой, что и , т. е. 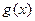является делителем .