Тема 8. Преобразование аффинных координат

Связь между радиус-векторами точки в различных системах отсчета   .   Формула связи ортов в трехмерном пространстве .   Формула связи координат в трехмерном пространстве .

Задачи к теме 8

8.1(658). Написать формулы перехода от одной системы координат к другой, если началом первой системы является вершина А параллелограмма ABCD, а базисом – векторы , ; началом второй системы является вершина С, а базисом – векторы , .

8.2(673). Даны две системы координат Oxyz и О'х'у'z'. По отношению к первой системе начало второй находится в точке О' = (2, 1, 3), а базисные векторы второй системы суть = (2, 4, 1), = (0, 4, 4), = (1, 1, 0).

1) Написать выражения координат точек относительно первой системы через их координаты во второй системе.

2) Выразить координаты точек относительно второй системы через их координаты в первой системе.

3) Найти координаты начала О и координаты базисных векторов , , 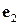первой системы относительно второй.

Справочный материал Преобразование прямоугольных координат на плоскости Рис. 8.1. Связь между радиус-векторами точки в различных системах отсчета Прямое преобразование координат при повороте и переносе системы координат