При повороте и переносе системы координат

Справочный материал

Преобразование координат, при котором все оси координат меняют свое направление на противоположное, называется инверсией координат.

Аксиальный вектор (псевдовектор) – величина, преобразующаяся как истинный (полярный) вектор при операциях поворота системы координат, но, в отличие от него, не меняющая свой знак при инверсии координат.

Простейшим примером аксиального вектора является векторное произведение, например, в механике – момент импульса.

8.3(674). Координаты х, у, z точек в системе Oxyz выражаются через координаты х', у', z' в системе O'x'y'z' соотношениями

,

,

.

1) Выразить координаты х', у', z' через координаты х, y, z.

2) Найти координаты начала О' и координаты базисными векторов , , второй системы относительно первой.

3) Найти координаты начала О и координаты базисных векторов , , 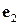первой системы относительно второй.

8.4(676). Найти координаты вершин тетраэдра ОABC в системе координат с началом в вершине О, базисными векторами которой являются медианы , , граней ВОС, СОA, AOB.

8.5(684). Написать формулы преобразования прямоугольных координат, если начало новой системы находится в точке О' = (–3, –2), угол от оси Ох до оси Ох' равен – и обе системы имеют противоположную ориентацию.

8.6(685). В системе Оху дана точка (6, –2); найти ее координаты в системе О'х'у', получающейся из системы Оху переносом начала в точку О' = (3, –4) и поворотом на угол – .