Умножение направленных отрезков на числа

Примеры умножения на числа:

Определение умножения направленного отрезка на число:

Задачи к теме 1

1.1(1). Векторы 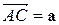и служат диагоналями параллелограмма ABCD. Выразить векторы , , и через векторы и .

1.2(4). В треугольнике ABC проведены медианы AD, BE и CF. Представить векторы , и в виде линейных комбинаций векторов и .

1.3(5). В треугольнике АВС проведены медианы , и . Найти сумму этих векторов.

1.4(8). Точки K и L служат серединами сторон BC и CD параллелограмма ABCD. Выразить векторы и через векторы и .

1.5(9). В плоскости треугольника ABC найти такую точку, чтобы сумма векторов, идущих из этой точки к вершинам треугольника, была равна нулю.

1.6(10). Дан четырехугольник ABCD. Найти такую точку М, чтобы .

1.7(13). Дан тетраэдр ABCD. Найти точку M, для которой .

Справочный материал

В геометрии точка приложения любого вектора , как правило, может быть выбрана произвольной. В соответствии с этим говорят, что геометрия изучает свободные векторы. В физике, кроме свободных векторов, встречаются также скользящие и связанные векторы.

Def: Скользящими называют такие векторы, которые считаются эквивалентными, если они не только равны, но и лежат на одной прямой (сила приложенная к абсолютно твердому телу).

Def: Связанными называются такие векторы, которые считаются эквивалентными, если они не только равны, но и имеют общее начало (силу приложенная к некоторой точке упругого тела).

1.8(17). Доказать, что сумма векторов, идущих из центра правильного многоугольника к его вершинам, равна .

1.9(22). Из точки О выходят два вектора, = , = . Найти какой-нибудь вектор = , идущий но биссектрисе угла АОВ.

1.10(25). Дан параллелепипед . Принимая за базис , и векторы , и , найти в этом базисе координаты векторов совпадающих с ребрами, диагональю параллелепипеда, диагоналями ребер, для которых вершина служит началом.

Справочный материал

1.11. Представьте направленный отрезок, соединяющий любые две точки на рисунке в виде линейной комбинации указанных на рисунке отрезков и . Например: . Попробуйте получить общую формулу для произвольного направленного отрезка:

.

1.12(32). Даны радиус-векторы , , и трех последовательных вершин параллелограмма. Найти радиус-вектор четвертой вершины этого параллелограмма.

1.13(33). Зная радиус-векторы , , и четырех вершин А, В, С, А' параллелепипеда ABCDA'B'C'D', найти радиус-векторы четырех остальных его вершин.

1.14(35). Даны радиус-векторы , и вершин треугольника АВС. Найти радиус-вектор точки пересечения его медиан. Где находится центр тяжести этого треугольника?

Тема 2. Система координат

Аффинная система координат

Декартовая система координат

Определение 2.1. Векторы () называются линейно независимыми, если линейная комбинация только в случае, когда все коэффициенты ().

Определение 2.2. Векторы () называются линейно зависимыми, если из них можно составить линейную комбинацию , в которой хотя бы один из коэффициентов не равен нулю .

Определение 2.3. Базис пространства – упорядоченный набор линейно независимых векторов, содержащий максимально возможное для данного пространства количество векторов.

Теорема 2.1. Разложение вектора пространства по базису этого пространства – единственно.

Теорема 2.2. При сложении векторов их координаты складываются, а при умножении на число – умножаются на это число:

,

.

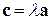
Задачи к теме 2

2.1(28). Установить, в каком из перечисленных ниже случаев тройка векторов , и будет линейно зависима, то есть когда один из векторов можно представить в виде линейной комбинации двух других:

а) , , ;

б) , , ;

в) , , .

2.2(30). Даны два вектора и . Найти проекцию вектора на плоскость при направлении проектирования, параллельном вектору .

2.3(31). Найти проекцию вектора на плоскость, определяемую векторами и при направлении проектирования, параллельном вектору .

2.4(50). Даны две смежные вершины А = (–1, 3), В = (2, 1) параллелограмма ABCD. Найти две другие его вершины при условии, что диагональ АС параллельна оси Ох, а диагональ BD параллельна оси Оу.

2.5(51). Даны три вершины параллелограмма (–2, 1), (1, 3), (4, 0). Найти четвертую его вершину D. Система координат (далее СК) аффинная.

2.6(56). В третьем октанте найти точку, зная, что ее расстояния до осей Ох, Оу, Oz равны соответственно 5; и . СК – прямоугольная.

2.7(59). Даны две точки А = (1, 2, 3), В = (7, 2, 5). На прямой АВ найти такую точку М, чтобы точки В и М были расположены по разные стороны от точки А и чтобы отрезок AM был вдвое длиннее отрезка АВ. СК – аффинная.

В последующих задачах этой темы СК – прямоугольная.

2.8(60). Дана окружность с центром в точке (6, 7) и радиусом 5. Из точки (7, 14) к этой окружности проведены касательные. Найти их длины.

2.9(61). Дана окружность радиуса 10 с центром (–4, 6). Найти точки ее пересечения с биссектрисами координатных углов.

2.10(62). Найти центр М и радиус r окружности, описанной около треугольника с вершинами (–2, –2), (2, 6), (5, –3).

2.11(66). Найти центр и радиус окружности, проходящей через точки (6,0) и (4, 0) и касающейся оси Оу.

2.12(70). Найти точку М, отстоящую от точки А = (–4, 0, 1) на расстояние 9, зная направляющие косинусы вектора : .

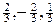2.13(72). Луч образует с осями Ох и Оу углы, соответственно равные и , а с осью Oz — тупой угол. Найти этот угол.

Тема 3. Деление отрезка в заданном отношении

Замечание. Если существует число , такое что , то точка лежит на прямой .

Задачи к теме 3

3.1(80). На оси координат даны три точки: А =(2), B =(7), С =(4). Найти:

1) отношение, в котором точка С делит отрезок ;

2) точку D, делящую отрезок в отношении –2/3;

3) середину E отрезка ;

4) отношение, в котором точка Е делит отрезок .

3.2(83). На оси координат даны три точки О =(0), Е = (1) и М = (х). Найти отношение, в котором точка О делит направленный отрезок .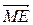

3.3(84*). На прямой даны три точки. Точка С делит направленный отрезок в отношении . Найти отношение, в котором каждая из точек А, B, С делит направленный отрезок, определяемый двумя другими.

3.4(85*). Пусть , , , причем . Найти отношение, в котором точка R делит отрезок .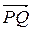

3.5(86*). Пусть , , . Найти отношение, в котором точка R делит отрезок .

3.6(91). Даны середины сторон треугольника (2, 4), (–3, 0), (2, 1). Найти его вершины. Система координат (СК) аффинная.

3.7(97). Даны две точки A = (9, –1) и B = (–2, 6). В каком отношении делит отрезок AB точка C пересечения прямой AB с биссектрисой второго и четвертого координатных углов? Система координат прямоугольная.

3.8(100). Дан треугольник с вершинами A = (4, 1), B = (7, 5), C = (–4, 7). Вычислить длину биссектрисы AD угла BAC. Система координат прямоугольная.

3.9(110). Найти отношение, в котором плоскость Oyz делит отрезок : A = (2, –1, 7) и B = (4,5, –2). Система координат аффинная.

3.10(111). Даны две точки A = (8, –6, 7) и B = (–20, 15, 10). Установить, пересекает ли прямая AB какую-набудь из осей координат.

3.11(112*). Даны четыре точки: А = (–3, 5, 15), В = (0, 0, 7), С = (2, –1, 4), D = (4, –3, 0). Установить, пересекаются ли прямые АВ и CD, и если пересекаются, то найти точку их пересечения. Система координат аффинная.

3.12(113*). Три последовательные вершины трапеции находятся в точках А = (–3, –2, –1), В = (1, 2, 3), С = (9, 6, 4). Найти четвертую вершину D этой трапеции, точку М пересечения ее диагоналей и точку S пересечения боковых сторон, зная, что длина основания AD равна 15. Система координат прямоугольная.