Задачи к теме 10

10.1(492). Дана точка A = (1, 2, 3).

1) Составить уравнения перпендикуляров, опущенных из точки А на координатные плоскости.

2) Написать уравнения перпендикуляров, опущенных из точки А на оси координат.

3) Написать уравнения плоскостей, проходящих через точку А и перпендикулярных к осям координат.

Система координат прямоугольная.

10.2(493). В пространстве дана прямая . Найти направляющий вектор этой прямой. Система координат аффинная.

10.3(498). Найти ортогональные проекции прямой на координатные плоскости Oyz, Ozx, Оху. Система координат прямоугольная.

Таблица 10.2. Уравнения плоскости

N	Название уравнения	Уравнение
1.	Общее уравнение
2.	Нормальное
3.	В отрезках
4.	Векторное параметрическое, заданное а) одной точкой и двумя векторами, б) тремя точками, в) двумя точками и одним вектором	, ,
5.	Параметрическое, заданное а) точкой и двумя направляющими векторами,     б) тремя точками,     в) двумя точками и одним направляющим вектором	, ,
6.	Векторное, заданное нормалью
7.	Векторное, заданное а) направляющими векторами, б) двумя точками и одним направляющим вектором, в) тремя точками	, ,
8.	Векторное уравнение плоскости в координатной записи, заданное а) направляющими векторами,   б) двумя точками и одним направляющим вектором,   в) тремя точками	, ,
Справочный материал   Нормаль к плоскости . Выражение нормального вектора через направляющие векторы: . Отрезки, отсекаемые на осях: , , . Абсолютное значение величины определяет расстояние от точки до прямой, а ее знак – их взаимное расположение.   Рис. 10.2. Параметры плоскости. Общее уравнение плоскости

Во всех последующих задачах этой темы система координат предполагается аффинной.

10.4(501*). Составить уравнения прямой, проходящей через точку
(3, –1, –4), пересекающей ось Оу и коллинеарной плоскости у + 2 z = 0.

10.5(508). Написать уравнение плоскости, проходящей через точку
(1, 2, 3), параллельной прямой x = y = z и отсекающей на осях Ох и Оу равные отрезки.

10.6(513). Составить уравнение плоскости, проходящей через прямую
x = 2 + 3 t, у = –1 + 6 t, z =4 t и коллинеарной прямой х = –1 + 2 t, y =3 t, z = – t.

10.7(516*). Написать уравнения прямой, проходящей через точку
(1, 2, 3) и пересекающей прямые

и .

10.8(520). Составить уравнения проекции прямой

из точки (1, 2, 1) на плоскость y – 2 z + 4 = 0.

10.9(526). Найти условия, необходимые и достаточные для того, чтобы прямая 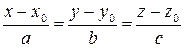: 1) пересекала плоскость Оху; 2) была параллельна ей; 3) лежала в этой плоскости.

10.10(530). Установить, какие из следующих пар плоскостей пересекаются, параллельны или совпадают:

1) 2 x + 3 у + 4 z –12 = 0, 3 x – 6 y + 1 = 0;

2) 3 x – 2 y – 3 z + 5 = 0, 9 х – 6 у – 9 z – 5 = 0;

3) 2 х – у – z – 3 = 0, 10 x – 5 у – 5 z – 15 = 0.

10.11(532). Установить, какие из следующих пар плоскостей пересекаются, параллельны или совпадают:

1) 2)

3)

10.12(534). Установить в каждом из следующих случаев, лежит ли данная прямая в данной плоскости, параллельна плоскости или пересекает ее; в последнем случае найти точку пересечения прямой и плоскости.

Прямая	Плоскость
1) ,	;
2) ,	;
3) ,	;
4) ,	.

10.13(539). Установить, какие из следующих пар прямых скрещиваются, параллельны, пересекаются или совпадают; если прямые параллельны, то написать уравнение плоскости, через них проходящей; если прямые пересекаются, то написать уравнение содержащей их плоскости и найти их общую точку.

1)	2)
3)	4)