 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Правило вычисления смешанного произведения
|
|
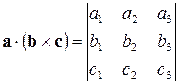 .
.
Для смешанного произведения имеет место равенство
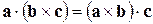 ,
,
которое позволяет записывать правило произведения трех векторов 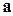 ,
,  и
и 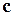 не указывая при этом, какие из двух векторов перемножаются векторно. При этом
не указывая при этом, какие из двух векторов перемножаются векторно. При этом
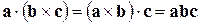 .
.
В силу приведенного выше равенства справедливо соотношение
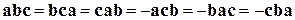 ,
,
согласно которому при циклических перестановках векторов смешанное произведение не меняется, а при перестановке двух векторов оно изменяет знак на противоположный.
Отметим, что необходимым и достаточным условием компланарности векторов 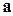 ,
,  и
и 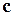 является равенство нулю их смешанного произведения:
является равенство нулю их смешанного произведения:
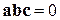
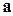 ,
,  и
и 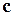 – компланарны.
– компланарны.
Правило раскрытия двойного векторного произведения:
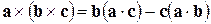 .
.
Двойное векторное произведение равно разности произведения среднего вектора на скалярное произведение остальных векторов и произведения другого вектора в скобках на скалярное произведение остальных векторов.
Задачи к теме 7
7.1. Представить заданный данный вектор 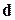 в виде разложения произвольного вектора по трем заданным некомпланарным векторам
в виде разложения произвольного вектора по трем заданным некомпланарным векторам 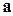 ,
,  и
и 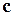 .
.
7.2. Упростить выражение
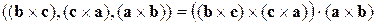 .
.
7.3(204*). Определить вектор 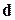 по заданным скалярным произведениям
по заданным скалярным произведениям 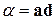 ,
, 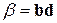 и
и  .
.
7.4. Найти компонент вектора 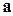 ортогональный вектору
ортогональный вектору 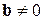 .
.
7.5(201*). Доказать тождества:
1) 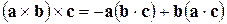 ; 2)
; 2) 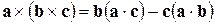 .
.
7.6(202*). Доказать тождества:
1) 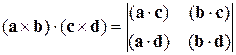 ;
;
2) 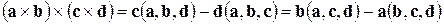 ;
;
3) 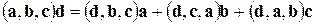 ;
;
4) 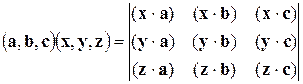 ;
;
5) 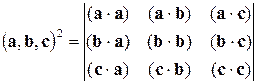 .
.
7.7(203*). Найти необходимое и достаточное условие для того, чтобы выполнялось равенство
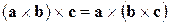 .
.
7.8(205*). 1) Найти необходимое и достаточное условие для того, чтобы уравнение 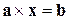 , где
, где 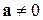 , имело решение.
, имело решение.
2) Найти общее решение этого уравнения.
7.9(206*). Даны три некомпланарных вектора 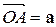 ,
, 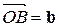 ,
, 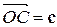 , отложенных от точки O. Найти вектор
, отложенных от точки O. Найти вектор 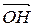 , где H – ортогональная проекция точки O на плоскость ABC.
, где H – ортогональная проекция точки O на плоскость ABC.
7.10(209*). Найти вектор х из системы уравнений 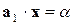 ,
, 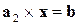 , где
, где 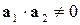 ,
, 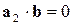 .
.
7.11(210*). Решить относительно х систему уравнений 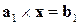 ,
, 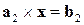 , причем
, причем 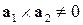 ,
, 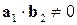 ,
, 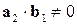 ,
, 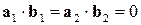 .
.
7.12(211*). Найти векторы 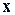 и
и  из системы уравнений:
из системы уравнений: 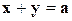 ,
, 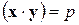 ,
, 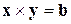 . Дано, что
. Дано, что 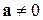 ,
, 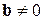 ,
, 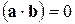 .
.
Дата публикования: 2015-11-01; Прочитано: 689 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
