 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тема 6. Векторное и смешанное произведение. Ориентации пространства
|
|
Векторным произведением векторов 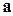 и
и  называется вектор
называется вектор  , определенный следующим образом:
, определенный следующим образом:
а) вектор 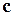 перпендикулярен и вектору
перпендикулярен и вектору 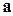 и вектору
и вектору  ;
;
б) длина вектора 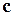 равна произведению длин векторов-сомножителей на синус угла между этими векторами;
равна произведению длин векторов-сомножителей на синус угла между этими векторами;
в) тройка векторов 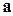 ,
,  и
и 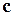 является правой;
является правой;
г) если  и (или)
и (или)  , то
, то  .
.
Вкратце определение векторного произведения не равных нулю векторов записывается так:


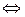

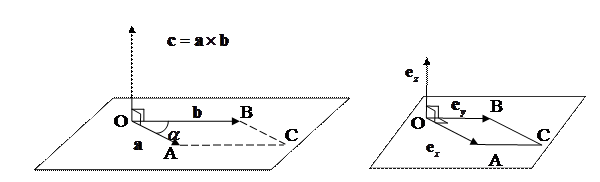

а) б)
Рис. 6.1. Векторное произведение векторов.
а) Определение векторного произведения  .
.
б) Векторное произведение ортов декартового базиса 
Правила раскрытия определителей
Двумерный определитель
 .
.
Трехмерный определитель
 .
.
Правило 1. Раскрытие по строке (по столбцу)

Правило 2


Правило 3
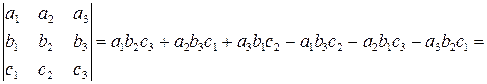


Правило 4
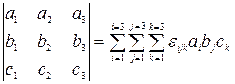 .
.
Задачи к теме 6
Во всех задачах этой темы система координат – прямоугольная.
6.1(176). Даны два вектора а = (1, 1, 1) и b = (1, 0, 0). Найти вектор с длины 1, перпендикулярный к вектору а, образующий с вектором b угол  и направленный так, чтобы упорядоченная тройка векторов а, b, с имела положительную ориентацию.
и направленный так, чтобы упорядоченная тройка векторов а, b, с имела положительную ориентацию.
6.2(178). Даны три вектора: а = (8, 4, 1), b = (2, –2, 1), с = (1, 1, 1). Найти вектор d длины 1, компланарный векторам а и b, перпендикулярный к вектору с и направленный так, чтобы упорядоченные тройки векторов а, b, с и а, d, с имели противоположную ориентацию.
6.3(189). Вычислить площадь треугольника, вершины которого находятся в точках A = (– 1, 0, –1), В = (0, 2, –3), С = (4, 4, 1).
6.4(190). Вычислить объем параллелепипеда ABCDA'В'C'D', зная его вершину А = (1, 2, 3) и концы выходящих из нее ребер В = (9, 6, 4), С = (3, 0, 4), A' = (5, 2, 6).
6.5(192*). Три вектора а, b, с связаны соотношениями  ,
,  ,
,  . Найти длины этих векторов и углы между ними.
. Найти длины этих векторов и углы между ними.
6.6(193*). Доказать, что если три вектора 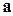 ,
,  ,
, 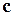 не коллинеарны, то из равенства
не коллинеарны, то из равенства  вытекает соотношение
вытекает соотношение  и обратно.
и обратно.
6.7(195*). Доказать, что если векторы  ,
,  ,
,  компланарны, то они коллинеарны.
компланарны, то они коллинеарны.
6.8(196*). Из одной точки проведены три некомпланарных вектора 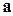 ,
,  ,
, 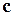 . Доказать, что плоскость, проходящая через концы этих векторов, перпендикулярна к вектору
. Доказать, что плоскость, проходящая через концы этих векторов, перпендикулярна к вектору 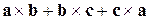 .
.
|

6.9(198*). Даны три некомпланарных вектора а = (х 1, у 1, z 1), b = (x 2, у 2, z 2), n = (А, В, С). Найти площадь параллелограмма, являющегося ортогональной проекцией на плоскость, перпендикулярную к вектору n, параллелограмма, построенного на векторах а и b.
6.10(200*). Доказать, что сумма векторов, перпендикулярных к граням тетраэдра, равных по абсолютной величине площадям этих граней и направленных в строну вершин, противолежащих граням, равна нулю.
6.11(207*). Доказать, что площадь параллелограмма, построенного на векторах а и b равна
 .
.
Справочный материал
Дата публикования: 2015-11-01; Прочитано: 1433 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

 .
2. Ассоциативность (сочетательное свойство):
.
2. Ассоциативность (сочетательное свойство):
 .
3. Дистрибутивность (распределительное свойство):
.
3. Дистрибутивность (распределительное свойство):
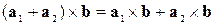 .
4. Параллельность векторов и векторное произведение
.
4. Параллельность векторов и векторное произведение

 .
5. Площадь параллелограмма и модуль векторного произведения
.
5. Площадь параллелограмма и модуль векторного произведения
 .
Векторное произведение в декартовом базисе
.
Векторное произведение в декартовом базисе
 ,
,
 .
Запись с помощью символа Леви-Чивита.
.
Запись с помощью символа Леви-Чивита.
 .
.
 Запись с использованием определителей второго порядка:
Запись с использованием определителей второго порядка:
 ,
,
 .
Запись с помощью определителя третьего порядка:
.
Запись с помощью определителя третьего порядка:
 .
.