Непрерывность обратной функции

Теорема 1. Пусть возрастающая (убывающая) функция непрерывна на отрезке 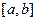. Тогда обратная функция также непрерывна.

Пример 1. Пусть функция определена на отрезке равенством . Очевидно непрерывна, возрастает и множество ее значений есть отрезок [-1,1]. Поэтому имеет обратную функцию, которая называется арксинусом и обозначается . Возрастающая функция задана на отрезке [-1,1], множество ее значений есть отрезок . Согласно Теореме 1 она является непрерывной.

Пример 2. Пусть функция определена на отрезке равенством . Очевидно непрерывна, убывает и множество ее значений есть отрезок [-1,1]. Поэтому имеет обратную функцию, которая называется арккосинусом и обозначается 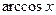. Убывающая функция 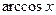задана на отрезке [-1,1], множество ее значений есть отрезок . Согласно Теореме 1 она является непрерывной.

Следствие 1. Пусть множество , на котором задана монотонная непрерывная функция , есть множество одного из следующих видов:

, .

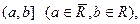
Тогда обратная функция также непрерывна.

Пример 3. Пусть функция задана на интервале равенством . Очевидно непрерывна, возрастает и множество ее значений есть вся числовая прямая. Поэтому имеет обратную функцию, которая называется арктангенсом и обозначается . Возрастающая функция задана на , множество ее значений есть интервал . Согласно Следствию 1 она является непрерывной.

Пример 4. Пусть функция задана на интервале равенством . Очевидно, непрерывна, убывает и множество ее значений есть вся числовая прямая. Поэтому имеет обратную функцию, которая называется арккотангенсом и обозначается . Убывающая функция задана на , множество ее значений есть интервал . Согласно Следствию 1 она является непрерывной.

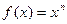Пример 5. Пусть функция задана равенством и имеет область определения , если 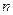есть нечетное натуральное число, и если 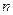есть четное натуральное число. Обратной к будет функция В первом случае ее областью определения будет , во втором– Согласно Следствию 1 она является непрерывной.

Пример 6. Функция есть обратная к функции 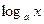, которая монотонна и непрерывна в своей области определения и множество значений которой есть вся числовая прямая. Согласно Следствию 1 функция , заданная на будет непрерывна в своей области определения.

20) Непрерывность элементарных функций.

Функции

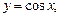
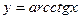называются простейшими (или основными) элементарными функциями. Функция называется элементарной, если она может быть получена с помощью конечного числа алгебраических операций и суперпозиций над простейшими элементарными функциями.

Совокупность всех элементарных функций называется классом элементарных функций.

Наряду с простейшими элементарными функциями широкое применение имеют так называемые гиперболические функции:

гиперболический синус

гиперболический косинус

гиперболический тангенс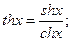

гиперболический котангенс

Теорема 1. Каждая элементарная функция непрерывна в любой точке своей области определения.