 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Таким образом, функции
|
|
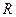 э
э 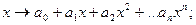
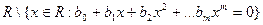 э
э 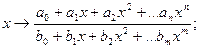
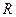 э
э 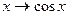 ;
;
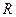 э
э 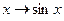 ;
;
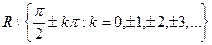 э
э 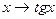 ;
;
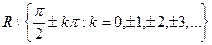 э
э 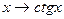
непрерывны в каждой точке своей области определения.
Предложение 1. Функция 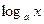 непрерывна в каждой точке своей области определения.
непрерывна в каждой точке своей области определения.
Доказательство: Будем считать для определенности, что 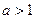 . Для
. Для 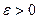 подберем
подберем 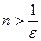 и положим
и положим 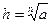 . Очевидно
. Очевидно 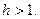 Так как
Так как 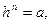 то
то 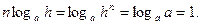 Поэтому
Поэтому 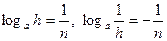 . Таким образом, в промежутке
. Таким образом, в промежутке 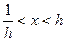 выполняется неравенство
выполняется неравенство 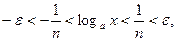 что и доказывает непрерывность функции
что и доказывает непрерывность функции 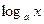 в точке
в точке 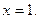
Пусть теперь 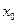 – произвольное положительное число,
– произвольное положительное число, 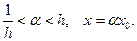 Тогда
Тогда
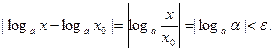
Так как интервал 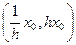 включает в себя некоторый интервал
включает в себя некоторый интервал 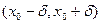 , то это доказывает непрерывность функции
, то это доказывает непрерывность функции 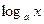 в точке
в точке 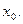
Используя второй замечательный предел, непрерывность функция 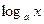 и теорему о пределесложной функции, можно доказать, что:
и теорему о пределесложной функции, можно доказать, что:
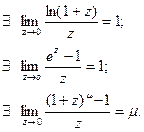
Теорема 1. Пусть 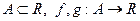 непрерывны в точке
непрерывны в точке 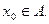 Тогда
Тогда 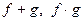 также непрерывны в точке
также непрерывны в точке 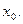 Если
Если 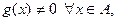 то и
то и 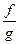 непрерывна в точке
непрерывна в точке 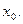
Теорема 2. Пусть 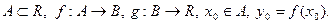 Если
Если  непрерывна в в точке
непрерывна в в точке 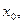 а
а 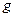 непрерывна в точке
непрерывна в точке 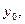 то сложная функция
то сложная функция 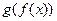 непрерывна в точке
непрерывна в точке 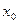 .
.
Дата публикования: 2015-09-18; Прочитано: 280 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
