Свойства функций, непрерывных на отрезке

Теорема 1 (Первая теорема Вейерштрасса). Непрерывная на отрезке 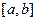(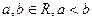) функция ограничена:  такое, что

Определение 1. Пусть Говорят, что функция принимает в точке наибольшее, или максимальное значение, если

Говорят, что функция принимает в точке наименьшее, или минимальное значение, если

Теорема 2 (Вторая теорема Вейерштрасса). Непрерывная отрезке 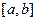() функция принимает в некоторых точках отрезка наибольшее и наименьшее значение.

Вторая теорема Вейерштрасса - это теорема существования, и неудивительно поэтому, что оно используется при доказательстве разного рода утверждений о существовании.

Пример 1. Из квадратного листа бумаги со стороной 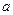см. будем делать открытые сверху коробки, вырезая для этого по углам листа равные квадраты и сгибая получившуюся крестовину. Докажите, что среди всех таких коробок есть коробка наибольшей вместимости.

Решение. Формализуем данную задачу – переведем ее на язык математики. Коробка наибольшей вместимости - это коробка наибольшего объема. Объем коробки, полученной описанным образом, равен , где 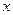–сторона вырезаемого квадрата— положительное число, меньшее . Поэтому надо доказать, что функция 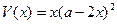рассматриваемая на интервале , принимает в некоторой точке этого интервала наибольшее значение. 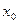По второй теореме Вейерштрасса непрерывная на отрезке функция в некоторой точке этого отрезка принимает наибольшее значение. Так как 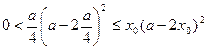, то , и тем самым При этом для будем иметь , а тогда

т.е. в точке 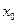функция 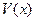принимает наибольшее значение. Следовательно, коробка наибольшей вместимости существует и получается при вырезании по углам листа квадратов со стороной 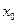см.

Теорема 3 (Коши о промежуточном значении). Пусть непрерывная на отрезке 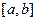функция, и – ее наибольшее и наименьшее значения, соответственно. Тогда

т.е. каждое число, заключенное между и есть значение функции в некоторой точке отрезка .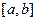

17) Критерий непрерывности монотонной функции, заданной на отрезке.

У монотонной функции разрывы могут быть только первого рода. Это замечание лежит в основе доказательства нижеследующей теоремы.

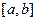Теорема 1. Для того чтобы монотонная функция , заданная на отрезке , была непрерывна, необходимо и достаточно, чтобы множество ее значений была отрезком.