Основные теоремы о пределах

Теорема1(Единственность предела). Если и , то .

Теорема 2(О сохранении знака). Пусть – предельная точка множества 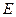. Предположим, что . Тогда , такая, что в каждой точке значение 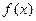функции положительно (отрицательно).

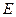Теорема 3 ( Предельный переход в неравенстве ). Пусть – предельная точка множества . Допустим, что существуют и . Если для , достаточно близких к 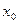и отличных от 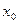, справедливо неравенство , то и .

Заметим, что строгое неравенство при предельном переходе не сохраняется.

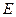Теорема 4 (Предельный переход и алгебраические операции). Пусть – предельная точка множества . Допустим, что существуют и . Тогда:

1)

2)

3) если и то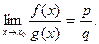

Теорема 5(Предел сложной функции). Пусть –

предельная точка множества A, 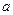–предельная точка множества 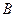, Предположим, что имеет место один из следующих двух случаев:

Случай 1: для отличных от 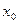, достаточно близких к .

Случай 2: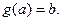

Тогда .

Случай 1 заведомо имеет место, если или Случай 2 имеет место тогда, когда функция 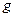непрерывна в точке 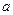(непрерывные функции изучаются ниже).