 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Предел монотонной функции
|
|
Определение 1. Говорят, что функция  ограниченасверху (снизу) на множестве
ограниченасверху (снизу) на множестве  если найдется
если найдется 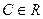 такое, что
такое, что 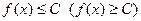 для любого
для любого 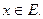
Теорема 1. Пусть  – неубывающая (невозрастающая) функция, заданная на множестве
– неубывающая (невозрастающая) функция, заданная на множестве 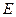 ,
, 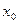 –предельная точка множества E, такая, что
–предельная точка множества E, такая, что 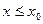 для любого
для любого 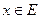 . Тогда
. Тогда 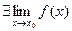 . Если функция
. Если функция  ограничена сверху (снизу) на множестве
ограничена сверху (снизу) на множестве  то этот предел конечен.
то этот предел конечен.
Теорема 2. Пусть  – неубывающая (невозрастающая) функция, заданная на множестве
– неубывающая (невозрастающая) функция, заданная на множестве 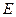 ,
, 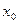 –предельная точка множества E, такая, что
–предельная точка множества E, такая, что 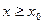 для любого
для любого 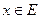 . Тогда
. Тогда 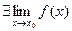 . Если функция
. Если функция  ограничена снизу (сверху) на множестве
ограничена снизу (сверху) на множестве  то этот предел конечен.
то этот предел конечен.
12)Число e.
Рассмотрим последовательность чисел

Имеем
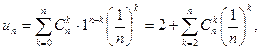
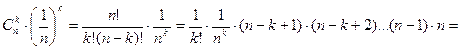
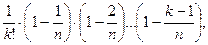
откуда
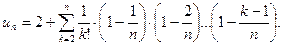
Тогда
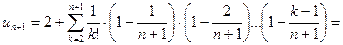
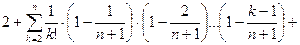
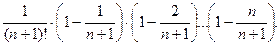
Таким образом, 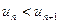 для любого
для любого 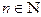 . Оценим сверху
. Оценим сверху 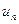 , заменяя
, заменяя  на 1. Учитывая, что
на 1. Учитывая, что 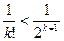 для
для 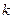 ≥ 2, имеем
≥ 2, имеем
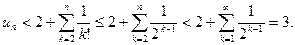
Согласно теореме о пределе монотонной функции существует конечный предел последовательности 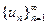 . Его обозначают через
. Его обозначают через 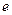 . Таким образом,
. Таким образом,
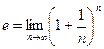 .
.
Дата публикования: 2015-09-18; Прочитано: 531 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
