Первый замечательный предел

Под первым замечательным пределом понимается предельное соотношение

. (1)

Для доказательства (1) прежде всего установим, что

. (2)

Действительно, площадь площади сектора площади .

Если через 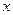обозначить радианную меру угла , так что длина дуги

выразиться произведением 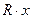, то эти неравенства перепишутся так:

.

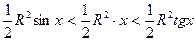Сократив на мы получаем (2). Из (2) получаем

,

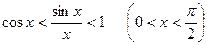откуда

.

Но , так что для .

Если , то по доказанному или .

Таким образом,

, если . (3)

Пусть теперь задано 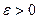. Выберем в качестве наименьшее из чисел и .

Тогда при , в силу (3), , что и доказывает (1).

Пример1. Пусть Тогда

Действительно,

Согласно (2)

Выберем 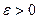и положим 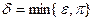. Пусть . Тогда

откуда

По определению предела это означает, что