 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Действительные числа
|
|
Символом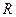 
мы будем обозначать множество всех действительных чисел. Множество 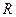называют также числовой прямой. Присоединим к 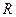два символа: 
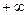и 
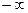, считая при этом, что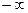 
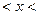
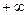для любого действительного числа 
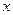. Полученное множество будем обозначать 
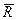и называть расширенной числовой прямой. Арифметические операции в 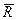не определяются.
Для любого действительного числа 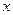найдется целое число 
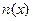такое, что
.
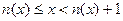Его называют целой частью 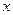и обозначают 
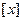. Согласно определению 
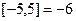, а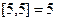 
. Очевидно 
.
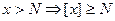Модуль (абсолютная величина) действительного числа 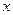определяется равенством
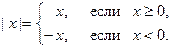
Для любых действительных чисел 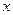и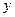 
имеем:
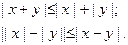
3) Бином Ньютона.
Для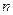 
натурального положим
= 
.
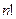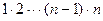Условимся также считать 0!=1. Очевидно,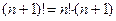 
. Для натурального 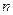и целого 
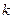, такого, что 
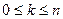положим
.
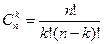Числа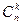 
называются биномиальными коэффициентами.
Теорема 1(Биномиальная теорема). Для любого натурального 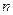и любых действительных чисел 
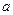и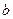 
справедливо равенство
.
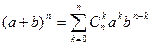Дата публикования: 2015-09-18; Прочитано: 224 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
