 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приклад 3. Нехай і не колінеарні вектори
|
|
Нехай  і
і 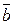 не колінеарні вектори. Довести, що вектори
не колінеарні вектори. Довести, що вектори  ,
,  і
і  лінійно залежні. Знайти коефіцієнти лінійної залежності.
лінійно залежні. Знайти коефіцієнти лінійної залежності.
Розв'язання: Вектори  ,
,  ,
,  лінійно залежні, якщо
лінійно залежні, якщо 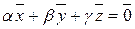 , а серед коефіцієнтів α, β, γ є відмінні від нуля.
, а серед коефіцієнтів α, β, γ є відмінні від нуля.
Перевіримо (підставимо в останню рівність розклади векторів  ,
,  і
і  за векторами
за векторами  і
і 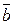 ):
):  .
.
 .
.
Так як  і
і 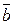 не колінеарні, то вони лінійно незалежні, отже, остання рівність можлива лише у випадку, коли коефіцієнти біля них рівнінулю:
не колінеарні, то вони лінійно незалежні, отже, остання рівність можлива лише у випадку, коли коефіцієнти біля них рівнінулю:
 Тому існує відмінна від нуля трійка дійсних чисел (-2γ, γ, γ), така, що
Тому існує відмінна від нуля трійка дійсних чисел (-2γ, γ, γ), така, що 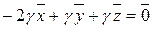 .
.
Знайдемо конкретні коефіцієнти. Покладемо, наприклад γ = -1, тоді α =2, β = -1. Маємо:  .
.
Базисом векторного простору називається така система векторів, яка:
1. задана в певному порядку;
2. лінійно незалежна;
3. будь-який вектор простору являється лінійною комбінацією цієї системи векторів.
Число елементів базису називається розмірністю даного векторного простору.
Базис системи колінеарних векторів складається тільки з одного вектора,  отже, він одновимірний.
отже, він одновимірний.
Лекція №3. Компланарні вектори. Розклад вектора за двома неколінеарними векторами. Розклад вектора за трьома некомпланарними векторами. Координати вектора.
Три вектора називаються компланарними, якщо вони лежать в одній площині, або паралельні до однієї площини.
Очевидно, що будь-які два вектора завжди компланарні, три вектора, два з яких колінеарні – компланарні.
Дата публикования: 2015-09-18; Прочитано: 235 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
